из точки К засекают сторону параллелограмма радиусом KF и через полученные точки G и Gj проводят прямые, параллельные линии KL. Эти прямые пересекают диагонали в точках 1, 2, 3 и 4, принадлежащих эллипсу. Точки 1, 2, 3 и 4 можно получить также, если отложить по направлению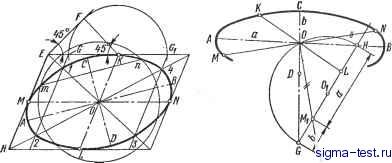

Рис. III.38. Построение эллипса по восьми точкам

Рис. III.39. Построение осей эллипса по сопряженным диаметрам

диагоналей отрезки 01 = OJOE и 02 = OJQH. Следует заметить, что диагонали параллелограмма не являются осями эллипса. Если требуется нанести оси построенного эллипса, надо пересечь эллипс какой-либо окружностью, описанной из центра О. Соединив точки пересечения тип хордой ши, проводят ось АВ\\тп и ось CD.

Построеше осей эллипса по данным сопряженсзым диаметрам (рис. III.39). Если даны сопряженные диаметры эллипса MN и KL, по ним можно построить обе оси эллипса АВ и CD, после чего построение самого эллипса может быть выполнено согласно рис. III.35 или III.36.

Через центр О проводят прямую ОЕ перпендикулярно к диаметру MN и откладывают на ней отрезок ОМ = ОМ - = ON. Через точку М и конец другого диаметра L проводят прямую и делят отрезок Л/jL пополам в точке Oj. Приняв эту точку за центр, описывают окружность радиусом ОО. Проведенная окружность пересекает продолжение прямой ML в двух точках G и Н, через которые проходят оси эллипса. Отрезок МуН равен большой полуоси эллипса, MjG - малой полуоси.

nocrpoeiffle эллипса по хордам (рис. Ш.40). Диаметр окружности аЬ делят на п равных частей (в нашем случае на шесть), через точки 7 и 2 проводят хорды параллельно диаметру cd. В заданных аксонометрических проекциях (например, косоугольной диметрической) изображают эти же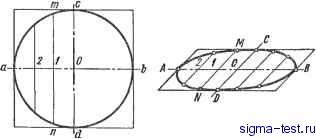

Рис. III.40. Построение эллипса по хордам

диаметры с учетом коэффициента искажения. Так, на рис. III.40 АВ - аЬ; CZ) = 0,5 cd. Диаметр АВ делят на то же число равных частей, что и диаметр аЬ, через полученные точки 1 и 2 проводят отрезки, параллельные линии CD, и откладывают на них отрезки, равные соответствующим хордам, умноженным на коэффициент искажения (в нашем случае MN = 0,5 тп и т. д.). Концы полученных отрезков соединяют плавной кривой линией.

Построе е в эллипсе диаметра KL, сопряженного данному диаметру MN (рис Ш.41). Для построения диаметра, сопряженного заданному диаметру MN, проводят в эллипсе какую-либо хорду EDW MN и, разделив ее пополам, находят точку С. Тогда диаметр KL, проведенный через точки О и С, будет сопряженным диаметру MN.

Построение касательной и нормали к эллипсу. Если заданная точка К расположена на эллипсе, построение можно осуш,ествить двумя способами. Первый способ (см. рис. Ш.35). Для построения касательной и нормали в точке К надо соединить точку К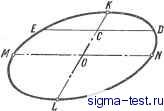

Рис. III.41. Построение диаметра АХ, сопряженного диаметру MN

С фокусами и разделить пополам угол между радиус-векторами ГК и FjK; биссектриса внутреннего угла F1KF2 яв- , ляется нормалью, а перпендикулярная к ней биссектриса внешнего угла - касательной.

Второй способ (рис. III.42). Через точку К проводят диаметр KL и строят сопряженный ему диаметр MP (для чего проводят какую-либо

хорду EG и KL и находят ее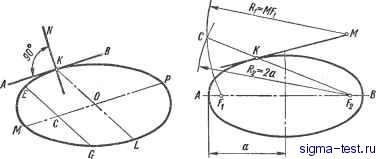

Рис. III.42. Построение касательной и нормали к эллипсу

Рис. Ш.43. Построение касательной к эллипсу, проходящей через внешнюю точку М

середину - точку С). Тогда прямая АВ 11 MP будет касательной к эллипсу в точке К, а прямая NK ± АВ - нормалью.

Если заданная точка Л/расположена вне эллипса (рис. 111143), построение производят следующим образом. Из точки М проводят через фокус fj дугу радиусом MFi = и из фокуса F2 - дугу радиусом R2 - 1а, где а - большая полуось эллипса. Соединив точку пересечения этих дуг С с фокусом F2, найдем точку касания К. (На практике касательная проводится обычно прикладыванием линейки к заданной точке Л/ и к контуру эллипса. Для уточнения положения точки касания следует пользоваться вышеописанным построением.)

Построение параболы. Ниже даны три варианта построения параболы: I) по заданным директрисе и фокусу (рис. III.44); 2) по данным вершине, оси и одной из точек параболы (рис. Ш.45); 3) с помощью касательных прямых к параболе (рис. Ш.46).

Вариант I (рис. Ш.44). Даны: директриса NO и фокус F. Для нахождения вершины параболы А расстояние от фокуса до директрисы делится пополам. Для построения других