3, 4, ... Во всех этих точках проводят касательные к кривой MN и откладывают на них равные отрезки произвольной длины: ААо = 1-Jq = 2-2q = 3-Зо==... Точки 1q, 2, 3q, ... соединяют плавной кривой KL. Далее строят нормаль к кривой MN в точке А и нормаль к кривой KL в точке Aq. Пересечение нормалей определяет точку О - искомый центр кривизны и отрезок OA - радиус кривизны для заданной точки. Плавная кривая, соединяющая центры кривизны для ряда точек кривой MN, называется эволютой кривой MN.

III.3. УКЛОНЫ и КОНУСНОСТИ

Уклоном прямой ВС относительно прямой АВ (рис. III.23,a) называется отношение

/ = h/l = tga.

Конусностью называется отношение разности диаметров двух нормальных сечений кругового конуса к расстоянию между ними (рис. 111.23,6). Таким образом, K={D-d)ll =2tga.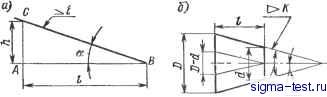

Рис. III.23. Уклон и конусность

Построекие уклонов. Если требуется через точку А, лежащую на прямой АВ (рис. III.24), провести прямую с уклоном i = 1: и относительно АВ, надо отложить от точки А по направлению данной прямой и произвольных единиц; в конце

полученного отрезка АЕ - восставить перпендикуляр ЕС длиной в одну единицу. Гипотенуза АС построенного прямоугольного тре-В угольника определяет искомую прямую.

Для проведения прямой с заданным уклоном 1: и через точку

Рис. III.24. Построение уклона через точку, лежащую на прямой

М, не лежащую на данной прямой АВ, можно поступать двояко (рис. III.25):

1) построить в стороне прямоугольный треугольник KLN (или LKNi) с отнощением катетов 1: и, причем катет KLW АВ; затем через точку М провести искомую прямую MD (или MDO параллельно гипотенузе KN (или LNi) вспомогательного треугольника;

2) опустить из точки М перпендикуляр МЕ на прямую АВ и, приняв его за единицу, отложить влево или вправо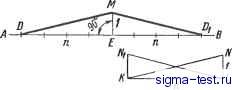

Рис. 111.25. Построение уклона через точку, не лежащую на прямой

от точки Е по направлению прямой АВ число и таких же отрезков; гипотенузы MD (или MDi) построенных таким образом прямоугольных треугольников являются искомыми прямыми.

Построение конусности. Построение конусности 1: п относительно данной оси сводится к построению уклонов I : In с каждой стороны оси.

111.4. ДЕЛЕНИЕ ОКРУЖНОСТИ НА РАВНЫЕ ЧАСТИ И ПОСТРОЕНИЕ ПРАВИЛЬНЫХ МНОГОУГОЛЬНИКОВ

Деление окружности на три равные части. Для построения точек, делящих окружность радиуса R на три равные части, достаточно из конца диаметра, например В (рис. III.26), провести дугу радиусом R. Эта дуга засекает на данной окружности две искомые точки 1 к 2; третьей точкой деления будет точка А на противоположном конце того же диаметра.

Деление окружности на четьфе равные части. Для нахождения точек, делящих окружность на четыре равные части, достаточно провести два взаимно перпендикулярных диаметра, например АВ и CD (рис. III.26).

Деление окружности иа шесть равных частей. Из концов какого-либо диаметра, например АВ (рис. Ш.27), необходимо провести как из центров две дуги радиусом R; полученные

точки пересечения 1, 2, 3 vi 4 вместе с концевыми точками диаметра АВ будут искомыми точками-деления.

Деление окружности на пять и десять равных частей. Проведя два взаимно перпендикулярных диаметра АВ и CD (рис. III.28), делят радиус 0D пополам в точке £; из точки Е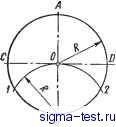

Рис. III.26. Деление окружности на три и четыре равные части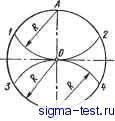

Рис. 111.27. Деление окружности на шесть равных частей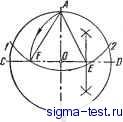

Рис. III.28. Деление окружности на пять и десять равных частей

Рис. III.29. Другой способ деления окружности на пять и десять равных частей

как из центра проводят дугу радиусом ЕА до пересечения ее с диаметром CD в точке F. Отрезок AF равен стороне Вписанного пятиугольника, т. е. делит окружность на пять равных частей. Отрезок OF равняется стороне десятиугольника и делит окружность на десять равных частей.

Другой способ деления окружности на пять и десять равных частей показан на рис. III.29. Проведя два взаимно перпендикулярных диаметра АВ и CD, делят радиус, например ОС, пополам в точке F и проводят прямую FB. Отклады-