вторая вспомогательная окружность радиусом i?} -i?2- Точка пересечения этих окружностей В определяет направление радиуса OjATi, идущего в точку касания. Для получения точки касания на второй окружности достаточно провести из центра Oj радиус OjKj параллельно радиусу ОКу ; остается соединить найденные точки касания прямой линией. Касательные к данным окружностям можно провести так же, как показано на рис. iii.13. в этом случае из центра большой окружности проводят вспомогательную окружность радиусом, равным сумме радиусов данных окружностей, т. е. Ri + Ri-

Построение окружности, проходящей через данную точку А и касающейся данной окружности (с центром О) в заданной точке В (рис. III.14 и 111.15). Через середину прямой АВ проводят перпендикуляр, в точке пересечения которого с линией ОВ получают центр Oj искомой окружности; радиус ее равен Оф или ОА.

Сопряжение окружности н прякшй при условии, что дуга сопряжения должна проходить через точку Л на прямой (рис. 111.16). Из данной точки А на прямой LM восставляется перпендикуляр к прямой LM; на его продолжении откладывается отрезок АВ, равный радиусу R окружности {АВ - R). Полученная таким образом

Даны:Ог,В,ЬМиА AB1LM AB=R АКЦО,В

точка В соединяется с центром окружности Oi, из точки А проводится прямая АК, параллельная линии BOi; пересечение ее с окружностью определит точку касания К искомой дуги сопряжения с окружностью. Остается продолжить отрезки OiK и АВ до их пересечения, чтобы найти центр О2 дуги сопряжения, а следовательно, и ее радиус.. Если пересечение прямых ОК и АВ получается под очень острым углом, то центр О2 можно найти

пересечением любой из них с перпендикуляром, проведенным через середину линии OjB (так как треугольник О2ВО1 - равнобедренный).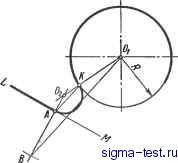

Рис. III. 16. Сопряжение окружности и прямой в заданной точке А на прямой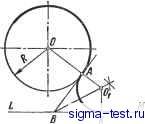

Рис. III. 17. Сопряжение окружности и прямой в точке А на окружности (внешнее касание)

Рис. III.18. Сопряжение окружности и прямой в точке А на окружности (внутреннее касание)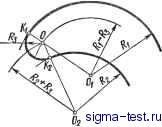

Рис. III.19. Сопряжение двух неконцентрических дуг окружностей дугой заданного радиуса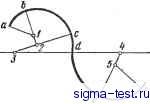

Рис. III.20. Вычерчивание кривой подбором дуг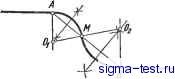

Рис. Ш.21. Сопряжение двух параллельных прямых двумя дугами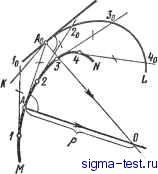

Рис. III.22. Построение центра и радиуса кривизны

Сопряжение окружности н npmwii при условии, что дуга сопряжения должна проходить через заданную точку А на окружности (рис. III.17 и Ш.18). Через точку А на окружности проводится к последней касательная АВ; угол, образуемый этой касательной и прямой LM, делится пополам. Пересечение биссектрисы угла АВМ с продолжением радиуса ОА определяет центр О у и радиус OiA искомой дуги сопряжения: Точкой сопряжения является точка К.

Сопряжение двух неконцентрических дуг окружностей дугой заданного радиуса (рис. III.19). Даны две дуги, описанные из центров Oi и О2 радиусами Л, и i?2- Для сопряжения их дугой заданного радиуса проводят из тех же центров две вспомогательные дуги радиусами Ri-Rj и R2 + Ry Пересечение этих дуг определяет искомый центр О. Точки касания Al и К2 находятся на линиях центров ОО2 и ОО.

Построение лекальной кривой подбором дуг (рис. III.20). Любая лекальная кривая может быть вычерчена циркулем путем подбора центров, из которых описываются дуги, совпадающие с отдельными участками кривой. Для того чтобы описываемые дуги плавно переходили одна в другую, необходимо, чтобы точки их сопряжения (касания) лежали на прямых, соединяющих центры. Построение ведут в следующем порядке: подобрав центр 1 для какого-либо участка кривой аЬ, подбирают центр 2 для следующего участка Ъс на продолжении радиуса, проходящего через точки b и 1; для участка cd подбирают центр 3 на продолжении радиуса, проходящего через точки с и 2, и т. д. Таким образом можно обвести всю кривую, не меняя лекала.

Сопряжение двух параллельных прямых двумя дугами (рис. III.21). Заданные на прямых точки А и В соединяются отрезком АВ, на котором отмечают произвольную точку М. В середине отрезков AM и ВМ проводят к ним перпендикуляры; в точках А и В также восставляют перпендикуляры к данным прямым. На пересечении соответствующих перпендикуляров находятся центры Oj и О2. Радиусы закругления: Ri = OiA; R2 = 02B. Касание дуг происходит в точке М, находящейся на линии центров О1О2. Если точку М выбрать на середине линии АВ, то Ry = Ro.

Построение центра н радиуса кривизны в точке, заданной на кривой (рис. III.22). Для построения в заданной точке Л кривой MN радиуса и центра кривизны отмечают на кривой в окрестности точки А несколько произвольных точек 1, 2,