S 7.1. Состав и шftemaшiфtljt сверхпрбвбдащих сплавов, полученных закалкой

Mi жидкого состояний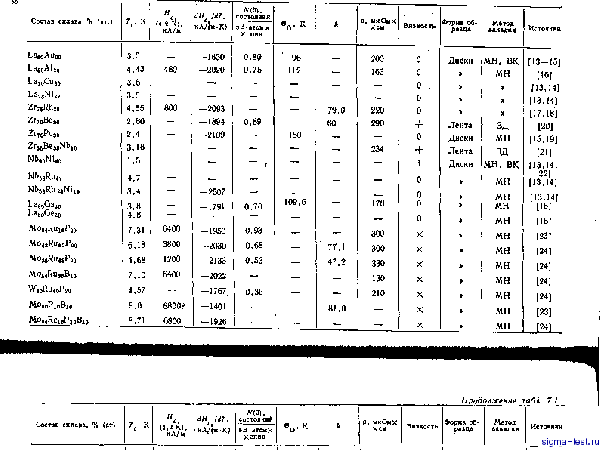

NbBBMo2eSi2o

NbgoMo3oSi2o

NbeoSiieB*

ЫЬвоЗЦгВв

NbgoSiieGei

NbsoSiieC*

NbeoZraoSiieB*

Nb4oMo4oSiieB4

TieNbsoSiis

TiisNbioSiiB

Ti4BNb4oSii2B3

TiesNbgoSiioBe

MOjoSiaoBjo

MojsSieBzo

W70SI20B10

ZreeSiie

ZrseNbeoSin ZrijNbjoSiie

4.9

2,71

3,56 3,82

2300

1280 640 480

2640 2720 3040 5750

6000 5200 640

-2308

-1910 -2229

-2308

-1910

-2070

-2300

-1727 -1671

0,40

0,37 0,35

229 231

72 69

190 180

+ + + +

+ + + +

X X X

Лента

ЗД ЗД ЗД ЗД ЗД ЗД ЗД ЗД ЗД ЭД

ЗД ЗД

[6] [6] [6] [6] [6]

[25]

[25]

[25]

[26]

[27]

[26]

[28.29]

[30 [30

Обозначения: Л(0) плотность электронных состояний на поверхногти Ферми; ® о - температура Дебая;

А -параметр Гинзбурга - Ландау; р-электрическое сопротивление; Н--возможна деформация изгибом на 180° с

плотным прилеганием концов образца; X - разрушение при изгибе; О - не установлело; МН-молота и наковальни; МВ - выстреливания капли; ЗД - закалка на диске.

вера-Хэммонда. Если у компонентов сплава наблюдаются значительные различия в значениях е/а, то Тс такого сплава, как правило, ниже значений критической температуры, полученных Коллве-ром и Хэммондом для сплавов соседних металлов, что, вероятно, связано с числом внешних d-электронов. На рис. 7.2 приведены также значения Тс для сплавов, полученных методом ионной имплантации. Эти значения практически лежат на кривой Коллвера-Хэммонда. Таким образом, можно сделать вывод, что Тс слабо за-BHcaiT от различий в способах получения аморфных сплавов.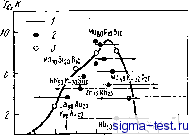

д и 5 6 18 9 fOe/a . (У) (Zr) (Nb){MO){Tc) (Ru) (Rh) (Pd)

Рнс. 7.2. Зависимость Тс аморфных сплавов, полученных криозакалкой, закалкой на жидкого состояния н ионной имплантацией, от электронной концентрации е/а (стрелками показаны составы сплавов, полученных

закалкой от жидкого состояния): / - пленочные сплавы после низкотемпературного напыления (данные Коллвера и Хэммонда); 2 - сплавы, полученные закалкой нз жидкого состояния; 3 - сплавы, полученные ионной имплантацией (данные Мейера)

о а 16 ги зг w X, % (am.)

Рнс. 7.3. Влияние металлоидов М на критическую температуру аморфных сплавов

(Mo6oRu )i-xiWx [24]: /-(MoeoRu4o), P,; 2-(Moe Ru4o)i j. Вд.; 5 - (MoeoRu4o)i j. As; 4 - (MoeoRu4o), . Si.; 5 - (Moeo Ru4o)i :Gej.

Критическая температура аморфных сплавов типа металл-металлоид зависит не только от сорта металлических атомов, но и от сорта и концентрации атомов металлоидов. На рис. 7.3 показано влияние металлоидов на Тс аморфного сплава M060RU40. Критическая температура снижается с увеличением концентрации металлоида и крутизна этого снижения уменьшается в р}1ду Ge, Si, As В P. В аморфных сплавах Ti - Nb интенсивность снижения Гс при легировании металлоидами возрастает в ряду В, Si, С, Ge [9], т е здесь наблюдается та же закономерность, что и в случае аморфных сплавов с молибденом.. Полагают, что такое снижение Гс связано с электроотрицательностью металлоидных атомов: чем выше электро-

отрицательность металлоида, тем больше вклад электронов переходных металлов в сверхпроводимость [24].

Однако несмотря на вышесказанное, интерес к сверхпроводящим аморфным сплавам возрастает, поскольку в этом случае появляется возможность получать материалы с превосходной прочностью и пластичностью. Сейчас уже известны следующие аморфные сверхпроводящие сплавы, которые можно деформировать изгибом на 180° с плотным прилеганием или подвергать холодной прокатке:

Nb7o 83Sii7-ai, NbsoSiio-zoBo-io. NbgoSiaeQei, NbgoSiieCi. Nbse-goMOo-teSiao. Nbgo-soMoo-soSiieBi, Ti45 7oNbi5 4oSii5, Tiio-ToNbig-isSiiaBs.

7.3. ФАКТОРЫ, КОНТРОЛИРУЮЩИЕ ВЕЛИЧИНУ Гс

Как было видно из рис. 7.1 и 7.2, имеется тесная связь между критической температурой аморфного сплава и электронной концентрацией е/а. Здесь мы кратко обсудим эту взаимосвязь.

Согласно Макмиллану 33] Гс зависит от нескольких параметров:

- 1,04(1 Н-Я,)

7 =: во /1,45 ехр

(7.1)

iX-fi*(l+0,62X,)J

гдевв - температура Дебая; [х*-параметр электрон-электронного взаимодействия, выражающий силу кулоновского взаимодействия; Я, -константа электрон-фононного взаимодействия:

Х, = Л(0)<Р>/М<(й2>, (7.2)

где Л(0) - плотность электронных состояний на поверхности Ферми; <Я> - средний квадрат элемента матрицы электрон-фононного рассеяния; М. - масса атома, <icu2> - средний квадрат числа фононных колебаний.

Из формул (7.1) и (7.2) видно, что Гс зависит от 0в и Я, [или Л(0)], поэтому для повышения Гс необходимо, чтобы величины во и Я, [или Л(0)] были большими. При этом нужно учесть, что зависимость Гс от Я. сильнее, чем от во-

Джонсон с сотр. [34] измерили магнитную восприимчивость х(Г) аморфных сплавов (Moi a;Rua;)8oP2o при различных температурах. Они установили температурно независимую составляющую магнитной восприимчивости Хо и> основываясь на предположении, что величина контролируется парамагнетизмом Паули, определяли Л(0) как Л(0) =%)/2[iB ([iB - магнетон Бора). Эта величина, как видно Из рис. 7.4, при увеличении концентрации рутения уменьшается от 0,93 до 0,37. Критическая температура Гс при этом также уменьшается в соответствии со снижением Л(0), т. е., как и следует из (7.1) и (7.2), между Л/(0) и Гс имеется тесная взаимосвязь.

Недавно на основе теории сильной связи в виде работ [28-30, 35, 36] по данным измерений величин {dHcJdT) р , модуля Юнга и плотности двойных Zr - (Si, Ge) и тройных Zr - Nb - (Si, Ge)

Величину <(u2> называют среднеквадратичной фононной частотой по Макмиллану. Ярмл . ред.

аморфных сплавов были рассчитаны Л/(0), к, во. Сопоставив зависимости этих величин и Тс от химического состава, авторы этих Т>абот показали, что в двойных сплавах Л (0) и Тс определяются в первую очередь концентрациями кремния и германия, а в трой-

Таблица 7.2. Критическая температура Тс, энергетическан щель До и коэффициент энергетическо{} щели 2Ао/квТс сверхпроводящих аморфных сплавов, полученных криозакалкой и методом распыления [37]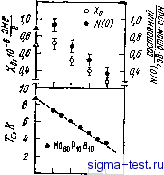

Сплав

т,. К

2Д, В-с

Nb,5Si25

NbjBGejg MogoNzo MoegSiaz

О iiZ 0,11 0,6 Ofi 1,0 (Mo) .x- (Rul

3,9 3,6 8,3 6,7

0,61 0,55 1,30 0,98

3,6 3,5 3,6 3,4

Рис. 7.4. Завнснмость критической температуры Гс, плотности электронных состояний на поверхности Фермн (0) и температур-но независимой составляющей магнитной проницаемости Хо от концентрации рутения в сплавах

(Mol-xRUx)8oP20 [34]

йых сплавах, кроме того, величина Я, контролируется также и содержанием ниобия. Эти результаты говорят о том, что аморфные сплавы, имеющие большие значения ЫЩ ХилиА,), имеют и высокую Тс.

Здесь учитывалось, правда, только то, что Тс зависит главным образом от yV(0) (или А.). Однако, как видно из (7.1) величина Тс кроме Л/(0) (или Я,) зависит также от температуры Дебая во, причем чем выше вп сплава, тем выше должна быть и Тс. К сожалению, сплавы с высокими значениями Л/(0) (или Я,), как правило, имеют довольно низкую температуру Дебая, и наоборот, сплавы с высокой во не всегда имеют достаточно большие значения Л/(0) (или %). Все же в последнем случае вероятность получения высокой критической температуры Тс больше.

Еще одним важным фактором, контролирующим сверхпроводимость, является величина энергетической щели До. Величина энергетической щели определялась в туннельных экспериментах на сплавах, полученных методами криозакалки и напыления [37]. Коэффициент энергетической щели (2До/йвГс), как видно из табл. 7.2, составляет --3,5. Это значение очень близко к величине 3,52, полученной по теории БКШ.

Г.4. КРИТИЧЕСКОЕ МАГНИТНОЕ ПОЛЕ Не И КРИТИЧЕСКАЯ ПЛОТНОСТЬ ЭЛЕКТРИЧЕСКОГО ТОКА Sc

Аморфные сплавы характеризуются отсутствием дальнего порядка в расположении атомов, поэтому их сверхпроводимость существенно зависит от величин Не и h. Сверхпроводники, у которых

длина свободного пробега электронов / меньше, чем длина когерентности \й{Т) =hvilnS<i [38] ipt - скорость Электронов на поверхности Ферми), называются грязными . В аморфных сплавах о(0) составляет 50-100 нм, а / - порядка межатомного расстояния. Следовательно, /<Со(0) и можно сказать, что аморфные сверхпроводники являются грязными сверхпроводниками второго рода. Как хорошо известно, в случае грязных сверхпроводников длина когерентности (т. е. протяженность области, в пределах которой при значительном пространственном изменении магнитного поля коэффициент энергетической щели существенно не меняется) обычно определяется следующим образом:

1(7) = 0,85 [ /7-,/(Г,-Г)] 1/2 . (7.3)

Глубина проникновения магнитного поля

Тс~т)

Х,(Т) = 0,615 A,jL (0)

(7.4)

где Яг,(0) -лондоновская глубина проникновения:

X(0) = (3cy8:iN (O)vf.e). (7.5)

Здесь с - скорость света. Отношение длины когерентности к глубине проникновения называют параметром Гинзбурга-Ландау. Этот параметр

k = k(T)/l{T) = O,725XL(0)/l. (7.6)

Поскольку, как уже указывалось, величина / в аморфных сверхпроводниках крайне мала, k становится очень большим (5()-1,00, см. табл. 7.1). По данным работ [29, 40] длина когерентности о составляет 3-10 нм, а А.(О)-200-=-1000 нм. Для аморфных сплавов критическое магнитное поле лежит между нижним критическим полем Яс, (Т) и верхним критическим полем НсЛТ), т. е. аморфные сплавы являются сверхпроводниками второго рода согласно теории ГЛАГ (Гинзбург-Ландау, Абрикосов-Горьков). По теории ГЛАГ величины Нс(Т), Нс,(Т) и HcT) связаны между собой следующим образом.:

Нс,=уТкН,(Т), (7.7)

Не, = (1/ V~2k) (logfe--0,08)Я,(7) , (7.8)

где Яс- Критическое поле при Ti=0 К.

Из этих соотношений можно видеть, что для аморфных сверхпроводников при большой величине к поле Не меньше Ясг и больше Яс,. Как видно из рис. 7.5, Яс увеличивается линейно с понижением температуры. Эта линейность обнаружена во многих аморфных сплавах. Теоретические кривые Маки [43] дают несколько завышенные значения Ясг. Таким образом, предложенные Маки (43] и Верт-хамером [44] модели не позволяют объяснить температурную зависимость Яс2 аморфных сплавов. Причиной этого может быть неупорядоченность атомных конфигураций как отличительная черта аморфных металлов, поэтому теоретическое изучение этого вопроса представляет несомненный интерес.

В идеальном сверхпроводнике второго рода пиннинг вихрей магнитного потока не происходит, а электрический ток нагрузки