ция металлоида составляет 24-2&%, кривые температура - электросопротивление имеют широкий пик при 100 К. Кроме того, электросопротивление имеет минимум в области температур 10- 20 К, причем рост сопротивления при более низких температурах составляет всего лишь iAip/ip= 10-10 *.

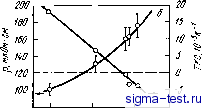too 2li0 Т,К

го го

Р,%(ат.)

Рис. 6.30. Характер изменений электросопротивления аморфных сплавов

Ni - Р, полученных электролитическим осаждением [46]: а - зависимость электросопротивления от температуры и содержания Р [цифры у кривых, % (ат.)]; бзавнснмость электросопротивления прн комнатной температуре и ТКС от содержания Р

Сплавы переходный металл - переходный металл

Электросопротивление аморфных сплавов Zr-Ni [50], Zr-Со [50];, Nb-i [51], RdZr ;[52, 53], Cu-Zr [54] и некоторых других до сих пор все еще является предметом пристального изучения. На рис. 6.31 показаны зависимости электросопротивления быстро-закаленных аморфных сплавов Nb-Ni от температуры и химического состава, полученные Нагелем i[51]. Величина ТКС этих сплавов отрицательна во всем диапазоне аморфизирующихся составов. Для электросопротивления аморфных сплавов третьей группы характерно то, что оно всегда! >200 мкОм-см. При этом наличие отрицательного ТКС при столь высоком сопротивлении ни в коем случае не является особенностью именно аморфных сплавов, поскольку эта закономерность часто наблюдается в кристаллических сплавах и тонких пленках. Между остаточным сопротивлением и ТКС многих аморфных и кристаллических сплавов существует взаимосвязь, аналогичная той, которая показана на рис. 6.32. Эта взаимосвязь носит название корреляции Муиджи [55]. Когда величина остаточного сопротивления крайне велика (20d мкОм-см), ТКС изменяется от малых положительных до малых отрицательных значений. Корреляция Муиджи сильнее, чем влияние упорядо-

Имеется в виду остаточное сопротивление. При , ред..

ченности атомных конфигураций в сплавах, что является существенной особенностью металлических материалов с высоким сопротивлением. Электросопротивление аморфных сплавов, принадлежащих к третьей группе, определяется в первую очередь корреляцией Муиджи.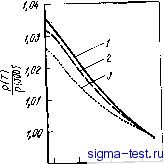

го 100 гоо зоот,к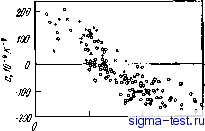

100 гоо

, р,М/(ОМ-СМ

Рнс. 6.32. Корреляция Муиджи между остаточным сопротивлением и ТКС [55

Рнс. 6.31. Завнснмость электросопротивления аморфных сплавов Ni-Nb от температуры и химического состава [51]:

; -Nb4Q Nieo; 2 - Nbso NIbo ; 3 - Nbeo №

Мацуда и Мидзутани [44] построили диаграмму (рис. 6.33), в которой сведены значения сопротивления и ТКС аморфных сплавов, входящих в группы 1-3, при температурах выше температур Дебая, Видно, что при высоком сопротивлении р200 мкОм-см ТКС<0, что, несомнеино, отвечает корреляции Муиджи. Мацуда и Мидзутани выдвинули предположение, что отрицательный ТКС при низком сопротивлении р<100 мкОм-см, наблюдаемый в аморфных сплавах Ag-Си-Ge и Mg-Zn, и отрицательный ТКС, характерный для жидких двухвалентных металлов таких, как цинк, обусловливаются действием одного и того же механизма.

Изменение электросопротивления вышеупомянутых аморфных сплавов может быть разделено иа четыре температурные области: T<Qd, QD<T<Tsat И Tsab<.T. Здесь Гтш -температура, при которой проявляется минимум электросопротивления (она обычно составляет 10-20 К), вг> -температура Дебая аморфного сплава, 7sa< -температура, при которой высокотемпературный ТКС начинает стремиться к насыщению, отклоняясь от закона Т или Р. Особенности пойедения электросопротивления и, в частности изменение знака ТКС, при отмеченных температурах иллюстрируются на рис. 6.34.

У аморфных сплавов с высоким сопротивлением, принадлежащих ко второй и третьей группам, если при высоких температурах Г>

>Tsat кристаллизация не происходит, сопротивление имеет тенденцию к насыщению, отклоняясь от закона ±Т или ±7 У аморфных сплавов, принадлежащих к первой или второй группам, при Qd< \<CT<Tsat ТКС изменяется по закону ±7]. При промежуточных температурах 7min<7<0D ТКС практически всех аморфных сплавов пропорционален ±Р. В области низких температур Г<Гт1п сопротивление аморфных сплавов пропорционально 1пТ и при снижении температуры повышается, однако скорость такого изменения сильно зависит от сорта компонентов аморфного сплава.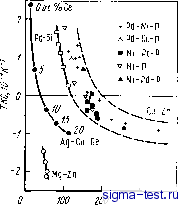

Рис. 6.33. Соотношение между электросопротивлением и ТКС различных аморфных сплавов [44;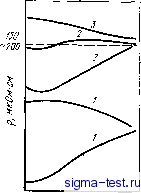

Рнс. 6.34. Температурные изменения электросопротивления аморфных сплавов относящихся к первой (/), второй (2) и третьей (3) группам

6.4.2. Теория электрического сопротивления Займана и ее модификации

Важным фактором, управляющим сложными закономерностями изменения электросопротивления аморфных сплавов, описанными в предыдущем разделе, является сорт компонентов сплава, причем в каждом температурном интервале этот фактор проявляется по-разному. До сих пор для объяснения этого привлекалась теория электросопротивления жидких металлов, в основе которой лежит учет взаимодействия электронов проводимости. В эту теорию внесены поправки, учитывающие, в зависимости от типа аморфного сплава и температурной области, наличие в аморфных сплавах различного рода дефектов. В этом разделе мы покажем, как с помощью теории Займана [56], позволяющей с успехом объяснить поведение сопротивления жидких металлов, можно также объяснить и некоторые особенности поведения электрического сопротивления аморфных сплавов, которые показаны на рис. 6.26, в

частности, непрерывность* изменения электросопротивления при переходе от жидкого к аморфному состоянию. Мы коснемся и некоторых усовершенствований теории Займана.

В основе теории Займана лежат следующие два положения

1. Распределение центров рассеяния электронов проводимости в жидком металле однородно, что подтверждается данными дифракции рентгеновских лучей и нейтронов.

2. Для вычисления псевдопотенциала слабых взаимодействий в жидком металле может быть использовано борновское приближение, что обусловливается тем, что в жидком металле ионы в достаточной степени экранированы электронами проводимости.

Когда электроны проводимости рассеиваются на ионах аморфного сплава, между ними происходит обмен импульсом й Q и энергией Йш. Вероятность рассеяния описывается динамическим структурным фактором S(Q), о), характеризующим пространственно-временную структуру аморфного сплава. Функцию 5(Q, со) называют также динамической функцией рассеяния или динамической интерференционной функцией. Динамический структурный фактор S(Q, (й) пропорционален статическому структурному фактору 5(Q), обычно определяемому в экспериментах по рентгеновской или нейтронной дифракции, который равен интегралу по энергии при постоянном Q в динамическом структурном факторе S{Q, со):

S(Q)= j S(Q, o))d<o.

(6.8)

Займан показал, что электросопротивление жидкого металла р может быть выражено через S(Q) следующим образом:

12nQo

2k р

QS(Q)\V(Q)\dQ,

(6.9-)

где e -заряд электрона; Qo-атомный объем; Vf и kp - скорость и волновое число электронов на поверхности Ферми; Q - вектор рассеяния и V<Q) - Фурье-компонента потенциала рассеяния ионов.

Эванс [57] усовершенствовал теорию Займана, заменив F(Q) на мaтpицy МТ - (muffin tin) - потенциала. В этом случае выражение (6.9) можно применить для описания также процессов рассеяния при сильных взаимодействиях в жидких переходных металлах:

V(Q)-v(Q) =

-2(2 + 1) sin Tinfifl

m (2m£/-)i/2 йо /

xPfCcose). (6.10)

где m - масса электрона; x\i{Ep)-фазовый сдвиг для рассеяния с угЛовым моментом /, вычисленный при энергии Ферми Ер. В бинарных сплавах S(Q) F(Q!) 12 заменяется на

1 См. примечание на с. 197. Прим. ред.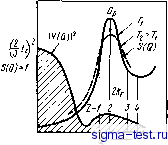

S (Q) 1VXQ) I < Гсплава = Ci <i p {ca + ci Su (Q)} + C2 1 {ca + x

X S22 (Q)} + Ci Сг ( <2 + <i 4) (Q) - 1Ь (6.11)

где Ci и t - концентрация и -матрица i-того компонента; ij(Q) - парциальный атомный фактор для пары i-/ [58].

Как видно из выражения (6.9), в теории Займана поведение р определяется поведением S{Q) и ]F(Q!)]2, На рис. 6.35 S(Q) и I V{Q) 2 схематично показаны как функции Q [60]. Вертикальные линии на рисунке соответствуют числу валентных электронов Z, как числу свободных электронов, приходящихся на один атом и

удвоенному, чтобы получить соответствие с фермиевскими волновыми числами. Другими словами, вертикальные линии отвечают положениям Q = 2kF. Фабер и Займан [59] предположили, что в двухвалентных металлах 2кр практически совпадает с положением главного максимума 5(Q)., т. е. с Qp. В случае 2=2 интеграл в уравнении (6.9), т. е. сопротивление р, уменьшается с повышением температуры. Действительно, в жидких двухвалентных металлах, например в цинке, ТКС становится отрицательным при температурах непосредственно над точкой плавления. Дл аморфных металлов, как и для жидких двухвалентных металлов, можно ожидать, что при выполнении условия Q 2if (условие Нагеля - Тауца) в области высоких температур. {T>Qd) ТКС может быть отрицательньвм.

Интересным является вопрос о том, действительно ли в аморфных сплавах реализуется условие Нагеля-Тауца или нет. Ферми-евское волновое число можно непосредственно измерить в экспериментах по комптоновскому рассеянию и аннигиляции позитронов. Кроме того, если можно воспользоваться моделью свободных электронов, то кр можно рассчитать из величины концентрации валентных электронов на атом (е/а) и атомного объема. К сожалению, аморфные сплавы, как правило , содержат большое число компонентов, наиболее важные из которых-переходные металлы, имеющие г-зону. Для них разделение внутренних и внешних валентных электронов неоднозначно, поэтому затруднено и определение kp по результатам комптоновского рассеяния и аннигиляции позитронов. Интересно, что поскольку упереходных и благородных металлов число валентных электронов Z=e/a меньше 2, то сплавлением их с поливалентными элементами, у которых Z-e/a больше 2, можно в конечном счете получить среднее число валентных электронов 2=2. В настоящее время почти не проводят непосредственные измерения kp в аморфных сплавах, содержащих переходные

Рис. 6.35. Схема, поясняющая основные положения теории [(ом. уравнение (6.9)1 электросопротивления жидких сплавов Займана [60]

металлы подгруппы железа, а вычисляют kp из предположения, что если ТКС<0, то 2 2.

В высокотемпературной области (Гбв), в жидких металлах, где энергия тепловых колебаний ионов много меньше энергии рассеяния электронов кТ, последние игнорируют движение ионов и рассеиваются упруго. Следовательно, в этом случае 8{Щ представляет собой в уравнении (6.9) статический структурный фактор, определяемый в экспериментах по рентгеновской или нейтронной дифракции. Однако нельзя игнорировать эффект неупругого рассеяния электронов за счет тепловых колебаний ионов. Поэтому, в уравнении (6.9) S(Q) нужно заменить на

j S{Q,ci>)f{k){l-f(P)}6(Ek-Ef,+n4>)d(i где /(&),- функция распределения Ферми. Так как [61]

/(*){l-f(fe)}6(£ft-fft + ft<B)=

to вклад неупругого рассеяния может быть представлен в виде

что добавляется к величине упругого рассеяния на поверхности Ферми. Тогда выражение для электросопротивления в теории Займана можно преобразовать с учетом эффектов неупругого рассеяния:

12JI Qo Jf й w . 3

о 1-0

S (Q, а>) kT й * 1

\t{Q)\

(6.12>

Если T>Qd, to поскольку

равенство (6.12) переходите (6.9).

Коут и Майзель [62, 63] показали, что если в S(Q,o)) учитывать только однофонный вклд, считая аморфный металл дебаевским твердым телом, то из расчета, что

SQ) =

S{Q, 0)) -

k Т ,Й-/* 1

d (В

(6.13)

- это {...} в выражении (6.12), можно объяснить особенности изменения ТКС аморфных сплавов. В результате расчетов получено, что