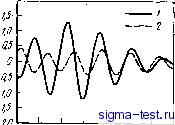спектра- поглощения атомов Си в сплаве CusZra, закаленном из жидкого состояния, обнаружили преимущественную группировку атомов Zr вокруг атомов Си. В этой работе проведено сравнение с

результатами, полученными в [12] методами нейтронной дифракции.

На рис. 3.21 показана зависимость величины k\{k) от k. Штриховая линия на рисунке соответствует формуле (3.25), в которой в расчет принимаются только парные корреляции Си-Си и Си-Zr в первой координациониой сфере. Получающиеся при таком подходе структурные параметры представлены в табл. 3.4. На рис. 3.22 показано равделение по парным корреляциям Си -Си и Си -Zr. Величины фазового сдвига и фактора обратного рассеяния, иепользоваНные в расчетах, получены теоретически [48, 49]. Как видно из табл. 3.4, применение методов ТСРП и изотопного замещения в нейтронной дифракции приводит к разным результатам при разделении парпых корреляций в аморфном сплаве CusZrj. В будущем важной задачей будет выяснение причин такого несовпадения при применении методов ТСРП и нейггронной дифракции, полученного на aMqpcb-ных сплав1ах Pd - Ge п Си-rZr.

Таблица 3.4. Параметры структуры аморфного сплава CuaZrs определенные методом jCPn г431 и параметры структуры аморфного сплава Си572г4з, полученные нейтронной дифракцией с использованием изотопного замещения [12]

4<7 5,0 6,0 7,0 8,0 9,0 ЩО K.l

Рис. 3.22. Корреляции Cuu (/) и Cu- -Zr (2), полученные разделением ТСРП края полосы поглощения меди в аморфном сплаве CujZra по уравнению (3.25) с оптимизацией

Параметр

ТСРП

Нейтронная дифракция {Cu572r<3: Мндзогутн и др.)

я, а

4,42

2,48±0,05

0,14±0,05

2,73±0,05

0,12±0,05 2,6Ii±0,5

2,65 2,80

5,4/5,0= 1,08±0,2

3.3. МОДЕЛИ СТРУКТУР АМОРФНЫХ ТЕЛ

3.3.1. Анализ структур случайной плотной упаковки (СПУ)

Рассматривая характерные особенности структуры аморфных твердых тел (рис. 3.7 или табл. 3.2), нельзя не задаться вопросом о том, какие же атомные конфигурации возникают в аморфных ме-

таллах? Ответ на этот вопрос не может быть получен из дифракционных экспериментов из-за недостаточной точности определения функций g{r). Даже эксперименты с привлечением метода ТСРП не позволяют дойти до трехмерной геометрической картины, давая только величину радиус-вектора атомов, окружающих данный конкретный атом.

Выходом из этого положения является построение и анализ различных моделей структуры аморфных металлов. Суть подхода состоит в том, что сначала составляется случайная плотная упаковка твердых сфер (СПУТС), затем определяется средняя плотность и парная функция распределения g{r) такой СПУ-структуры, после чего с использованием подходящего парного потенциала или надлежащих геометрических условий, или и того, и другого вычисляются локальные смещения в атомных конфигурациях, в результате чего происходит стабилизация модели СПУ-структуры.

Модели СПУ-структур привлекались, в первую очередь Берна-лом [50], для изучения стро.ения жидкостей. Бернал, а затем Фин-ней [51] предложили способ построения моделей, заключающийся в том, что в резиновый мешочек плотно набиваются стальные шарики и мешочек затем сжимается. Подобная геометрическая модель может просчитываться на ЭВМ по различным алгоритмам, чек! создается многообразие СПУ-структур:

Бернал считал, что трехмерные Связи в СПУ-структуре можно представить в виде различных многогранников. Он выяснил, каковы эти многогранники и в каких соотношениях они содержатся в СПУ-структурах. Если допустить, что колебания длины сторон полиэдров составляют до 15%, то СПУ-структура может быт)ь сбстав-лена из пяти типов полиэдров (рис. 3.23). Поры в этих полиэдрах называются дырками Бернала. Размеры дырок Бернала в полиэдрах всех пяти типов и количественные соотношения между полиэдрами разных типов представлены в табл. 3.5. Правильные тетраэдр (рис. 3.23, а) и октаэдр (рис. 3.23, б) составляют структуру плотно-упакованных О.Ц.К., г.ц.к. и других кристаллов, а тригональная призма (рис 3.23,в), архимедова антипризма (рис. 3.23,г) и тетрагональный додекаэдр (рис. 3.2, д) характерны для аморфных структуре

Финней построил модель структуры СПУ, составленной приблизительно из 8000 жестких шаров, и для объяснения особенностей полученной геометрической структуры провел анализ полиэдров Вороного. Полиэдр Вороного определяется как многогранник, построенный следующим образом: центр данного атома соединяется отрезками с центрами соседних соприкасающихся с ним атомов: перпендикулярно этим отрезкам в их середине проводятся плоскости. С помощью такого многогранника и описывается локальная геометрическая конфигурация атомов, расположенных вокруг цен-

Это так называемые некристаллографические полиэдры (ячейки) Бернала. Ярол(. ред.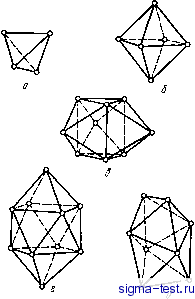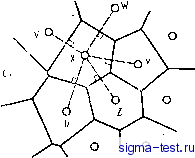

Рис. 3.24. Построение двумерного многоугольника Вороного вокруг атома X

Рис. 3.23. Пять типов полиэдров Бернала в модельных СПУ-структурах (см. текст) [50]

трального атома. В качестве примера на рис. 3.24 показано построение двухмерного многоугольника Вороного. Полиэдры Вороного в правильных кристаллических структурах по своему физическому смыслу соответствуют ячейкам Вигнера - Зейтца. На рис. 3.25 показаны полиэдры Вороного для г.ц.к. и о.ц.к. кристаллов.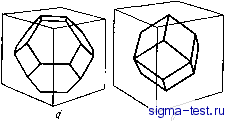

Рис. 3.25. Полиэдр Вороного для о, ц.к, структуры [0; 6; 0,8] (а) и г.ц.к. структуры [0; 12; Щ (б)

Отдельный полиэдр Вороного может быть описан совокупностью чисел П{ равных числу граней, имеющих i ребер: (пз, 4, П5...). Так, показанные на рис. 3.25 ячейки Вигнера - Зейтца для о.ц.к. и г.ц.к. кристаллов могут быть выражены соответственно, как (0,6,0,8) и (0,12,0). Финней показал, что среднее число граней по-лиэдров Вороного в моделях СПУ-структур составляет Np = = 14,251+0,015. Эта величина отличается от значений для г\ц.к. и о.цж. структур в кристаллах, составляющих соответственно Af = 12 и iVj=14. На рис. 3.26 приведены результаты Финнея по

определению числа ребер граней полиэдров Вороного в модельных СПУ-структур ах. Среднее число ребер составило Aff = 5,158+ ±0,003. Получилось, что в полиэдрах преобладают пятиугольные грани, что не соответствует обычным кристаллическим структурам.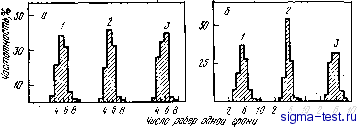

Рис. 3.26. Распределение числа ребер в одной грани полиэдра

Вороного в моделях СПУ-структур: а - СПУ-структура Финнея [51]; / - жесткие сферы Бернала; 2 -структура Бернала после релаксации; 3-(l-j)-

кристалл (при температуре плавления); б - СПУ-структура Ямамото [10, 54]; 1 - др релаксации; 2 -после релаксации; 3 - жидкость

Порядок укладки атомов, рассчитанный ЭВМ, если судить по парной функции распределения в модели СПУ-структуры, значительно изменяется в процессе релаксации, что следует из рис. 3.27. Видно, что высота плеча второго

пика функции g{r) в модели Таблица 3.5. Размеры централь-

, Д\, иых пор ДЛЯ различных типов поли-

СПУ-структуры Финнея не очень р, в модели СПУТС Бернала [50] хорошо воспроизводится экспериментально. Как указывается в работах [52, 53], высоты второго пика g{r) и его плеча строго ограничены в своих .изменениях (что показано экспериментально), а их координаты связаны соотношениями Г2/г 1 = 1,67 и Гз/Г1 = = 1,93, поэтому важным элементом .релаксированной СПУ-структуры может быть искаженный тетраэдр.

В связи с этим Ичикава-при помощи ЭВМ построил модель СПУ-структуры путем последовательного помещения жестких ша-

Из всех позиций, отвечающих условию Ичикавы, выбирается та, которая находится ближе всего к центру начальной структурной единицы (так называемый глобальный критерий, обеспечивающий сферичность создаваемой глобулы). Отметим также, что условие ft= Г отвечает идеальным, неискаженным тетраэдрам. Прим. ред.

ров в положения плотного контакта с тремя такими жесткими шарами диаметром а, расстояния между которыми меньше ka (если назвать k параметром тетраэдра, то может принимать значения lyfel). Им была построена и проанализирована модель СПУ-структуры, которая получается повторением операции укладки жестких сфер в тетраэдры. Оказалось, что для того, чтобы расчетные параметры вторых пиков g{r) были близки к полученным экспери-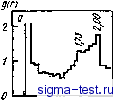

J-1 L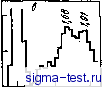

J L.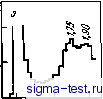

iff if. 2,0

1,0 1,5 2,0

1,0 1,5 2,0

Рис. 3.27. Парная функция распределения для различных моделей СПУ-структур; цифрами указано положение плеча второго пика &{г)-гГх и гг-. fl -модель Беннета (всеобщий глобальный, обобщенный) критерий; б-модель Беннета (локальный критерий); в - модель Беннета с релаксацией по потенциалу Морзе; г - высокоплотный кластер из жестких сфер; д - политетраэдр ическая модель; е - модель Финнея; ж - модель Финнея с релаксацией по потенциалу Леннарда-Джонса; з - модель Фиинея, построенная методом молекулярной динамики с использованием потенциала Леннарда-

Джонса

ментально на напыленной аморфной железной пленке, необходимо ввести ограничение 1,2. Однако, если при таком ограничении укрупнить модель, доводя количество укладываемых сфер до тысячи, возникает большое число пор и средняя плотность структуры снижается до 70-80% от средней плотности при малом числе сфер.

Во избежание этого Ямамото с сотр. [10, 54] построили модель СПУ-структуры, аналогичную модели Ичикавы, с А = 2, а затем

применили к этой модели релаксационную процедуру с использованием парного потенциала Пак-Дояма. При этом, как видно из рис. 3.28 и табл. 3.2, средняя плотность функции g(r) и S(Q) оказались близки к экспериментальным значениям. Результаты Ямамото и сотрудников по анализу полиэдров Вороного в моделях СПУ-структуры приведены в табл. 3,6 и на рис. 3.26,6. Для срав-

Рис. 3.28. Парная функция распределения g(r) и интерференционная функция S(Q) в модели Cny-CTpjTCTypbi

Ямамото [10, 54]: а, б -без релаксации; в, г-после релаксации с использованием парного потенциала Пак-Дояма; 1 - экспериментальные значения; 2 - после релаксации

sm г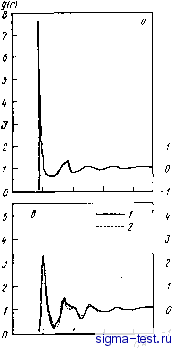

0,0 2,5 5,0 7,5

нения на рис. 3.26, а показаны результаты анализа модели структуры СПУТС Финнея с релаксацией СПУ-структуры по потенциалу Леннарда - Джонса. Финней считает, что поскольку пятиугольные грани полиэдров Вороного в структурах аморфных тел встречаются наиболее часто, атомные конфигурации в таких структурах представляют собой несколько измененные икосаэдры из 13 атомов (рис. 3.29). Правильные 13-атомные икосаэдры могут быть описаны как (0,0,12), они имеют пятиугольные грани и сохраняют в структуре высокий коэффициент заполнения, близкий к таковому для г.ц.к. кристаллов. В работе [10] проведено моделирование структуры жидкого железа выше точки плавления, которая сравнивается со структурой аморфного твердого тела. Результаты работы [10] подтверждают высказанные выше соображения.

На рис. 3.30 представлены результаты анализа сечений поли-