в результате проведенного исследования [6] с помощью ЭВМ построено изменение парной функции распределения g(r) с температурой в процессе быстрого охлаждения жидкого аргона со скоростью 1012-1013 К/с (рис. 3.6). Физический смысл g(r) состоит в том, что она описывает вероятность, с какой соседний атом Аг может находиться на расстоянии г от центрального атома Аг.

Вблизи температуры плавления (Г =83,75 К) функция g(r) аргона практически аналогична g(r), наблюдаемой для обычного , жидкого металла.- Характерно, что

первый пик g{r) острый и довольно высокий (2,5-3), а второй пик имеет заметную ширину. С понижением температуры положение пиков практически не изменяется, однако первый пик функции g{r) все более заостряется, а второй начинает распадаться на два. При Г<22,3 К разделение второго пика g{r) в аргоне, также как и в аморфных сплавах, можно обнаружить методами рентгеновской дифракции.

На рис. 3.7,6 показано сравнение парных функций распределения g{r) аморфной железной пленки, изготовленной напылением при сверхнизких температурах [7], и жидкого железа при температуре непосредственно над точкой плавления [8].. Положения первых пиков g (г) аморфной пленки и жидкого металла практически одинаковы, однако в первом случае пик значительно острее. Кроме того, в отличие от жидкого железа, второй пик g{r) аморфной пленки распадается на два, имеющих различную высоту. Что касается третьего и последующих пиков функции g(r) аморф-

s(a) 3

г о г о г о г о г о

3.0 3.5

1,5 2,0 г, 3,033А

Рис. 3.6. Изменения парной функции распределения g(r) в зависимости от температуры при охлаждении жидкого аргона со скоростями 1012-1013 к/с [6i]

15 а,А-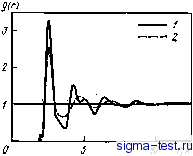

Рис. 3.7. Интерференционная функция S(Q) и парная функция распределения g{r) аморфной железной пленки {Г) [7] и жидкого железа при 1560°С (2) [8]

ной пленки, то они значительно смещены в сторону больших значений т относительно пиков, соответствующих жидкому железу, а декремент затухания их осцилляции мал. По-видимому, представленная на рис. 3.7 функция g{r) аморфной пленки не соответствует чистому аморфному железу, поскольку обычно в аморфных пленках, изготавливаемых напылением, присутствуют заметные количества примесей кислорода и азота. В случае же быстроохлажден-ного жидкого аргона значения g{r), рассчитанные на ЭВМ, хорошо совпадают с экспериментальными данными (рис. 3.6).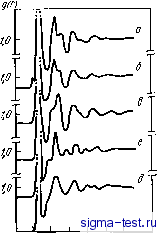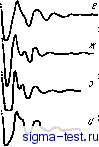

л L

О г ll 6 8 10 12 г А

о г If в а

12 г,А

Рис. 3.8. Парная функция распределения g{r) [9]: а-аморфная железная пленка (эксперимент); б -никелевая аморфная пленка (эксперимент); е-о. ц. к.; г - г. ц. к.; д - т.п.; е -о. ц. т.; яс -А-15; з и -СПУТС

Анализ координат пиков g(r) показывает, что аморфное состояние существенно отличается от жидкого состояния даже вблизи точки плавления, не говоря уже о классических г. ц. к. и о. ц. к. кристаллах. На рис. 3.8 показано сравнение функций g(r) для аморфных железных и никелевых пленок, полученных напылением, с g(r) для различных кристаллических структур [9]. В табл. 3.2 приведены значения координат всех пиков g(r), начиная со второго, в отношении к координате первого пика Гп/ri {п - порядковый номер пика). Видно, что для аморфных структур характерно отношение r2/ri=l,6-f-1.7.

Следует обратить внимание читателей, что функция g{r) для кристаллических структур - это не .результат эксперимента, а расчетные данные, очевид-

но, полученные для .моделей су&микроскопических частиц. Прим. ред.

Таблица 3.1. Температура плавления Тт, температура стеклования Tg, температура кристаллизации Тх и критическая скорость охлаждения Rc сплавов, аморфизируемых при закалке из жидкого состояния

Аморфный сплав

Коэффициенты уравнения Фогеля - Фулчера

По. кПа-с

В, К

Гс. К

Таблица 3.2. Координаты пиков r lri парной функции распределения g{r) для жидкого, аморфного и кристаллического состояний и коэффициент заполнения Т]

3.2. ИЗУЧЕНИЕ СТРУКТУРЫ БЛИЖНЕГО ПОРЯДКА В АМ01>ФНЫХ СПЛАВАХ

3.2.1. Парная функция распределения и интерференционная функция

Парная функция распределения для жидкого и аморфного металла g(r) может быть получена в экспериментах по дифракции рентгеновского, нейтронного или какого-либо другого излучения с

длиной волны порядка межатомного расстояния (см. 3.1.3). В этом случае интенсивность когерентного рассеяния рентгеновских лучей

или нейтронов hoh(Q) на образце; содержащем N атомов, может быть выражена как

N N

icoh (Q) = < 2 2 Q( n-i) )>. (3-12)

где <...>-усреднение по времени; bi(bj) я ri(rj) - соответственно амплитуда рассеяния излучения и величина вектора,

описывающего положение i(j)-roro атома; Q - вектор рассеяния. При упругом рассеянии на изотропном образце жидкого или аморфного металла Q = Q = (4лД) sin 9.

Как видно из рис. 3.9, излучение с длирой волны X и волновым

числом \ko \ = 2п/1 рассеивается под углом 29. Волновое число рассеянного излучения \к\л2п[К и изменение импульса при рассея-ниий Q=fl(k - ko)Icoh(Q) являются функциями Q. Экспериментально величина Q определяется через X или 29. Если посредством монохроматизации обеспечивается постоянная длина волны излучения,

то Icoh(Q) определяется как функция угла рассеяния 29. Другой способ, который в последнее время находит все большее применение для исследования жидких и аморфных веществ состоит в изменении длины волны X, при этом учитывается энергия непрерывного белого излучения: при фиксированном угле 29 из)меняется X и по спектру энергии

можно судить об изменении Q.

Для жидких и аморфных металлов, после усреднения величин Q и

ri - rj=rij по углам, выражение (3.12) можно упростить следующим образом.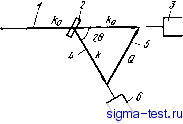

Рис. 3.9. Схема измерения /сой (Q) в экспериментах по

дифракции: 1 - падающий луч; 2 - образец; 3 - регистратор падающего излучения; 4 - рассеянный луч; 5 - вектор рассеяния; 6 - счетчик

/=1/=1 ч

(3.13)

Здесь rij= rij\ = \ri - rj\. Выражение (3.13) известно как формула Дебая. Можно считать, что в образце, имеющем М атомов, амплитуда атомного рассеяния одинакова для всех атомов. Если считать, что bi = bj = b, то (3.13) преобразуется в

3 Зак, 307

(3.14)

hoh (Q) = Af62 С 1 + 2

Здесь под 2 подразумевается суммирование по всем за исключением rij=0.

Теперь, если расстояние между данным атомом и начальной точкой г определить через функцию g(r), то в (3.14) сумму можно заменить интегралом, и тогда

hoh (Q) = т

sinQ г

1 + j 4яг2ро g(r) о

\+Unrpg{r) о

SinQ г sinQr

dr+, 4яг2ро -::-dz

(3.15)

(3.16)

Поскольку объем образца много больше объема атома, то интеграл берется по всему образцу (О, оо). Здесь ро - средняя плотность. При Q = 0 сомножитель в квадратных скобках превращается в функцию 6(Q), вклад которой в интенсивность экспериментально определить невозможно.

hoh(Q) - интенсивность рассеянного излучения, которую мож но измерить экспериментально. Если определить интерференционную функцию S(Q) как

S{Q)=Icoh{Q)/Nb, (3.17)

то из (3.16) можно получить

с sin о г

S(Q)-1 + J 4яг2р и(г)--1}- dr.

(3.18)

Равенство (3.18) является основной формулой, связывающей измеряемую непосредственно в дифракционных экспериментах интерференционную функцию S(Q) с парной функцией распределения g(r). Функцию S(Q) часто также называют структурным фактором. Реально сначала определяют функцию S(Q)j по которой можно затем различным образом найти g(r):

(-) = 1 +

2 Я2 Ро

7(5 (Q)

l}QsmQrdr.

(3.19)

Представим атом, находящийся в некоторой начальной точке, сферой радиусом г, ведя отсчет от ее геометрического центра. Распределение плотности атомов, находящихся на внешней поверхности этой сферы, определяется как функция радиального распределения (ФРР) и равно 4nr2pog(r).

При экспериментальном определении интенсивности рассеянного когерентного излучения используются многочисленные довольно сложные поправки. Кроме того, погрешность при определении S(Q) накладывается на погрешность, связанную с некоторой неопределенностью области интегрирования по Q, что безусловно

влияет на ошибку определения g(r). Требование высокой точности определения g(r) отнюдь не означает, что эта точность легко достижима. Тем не менее определенный опыт проведения экспериментальных процедур уже накоплен.

3.2.2. Изучение локальной структуры аморфных сплавов путем определения парциальных функций рассеяния

Стабильные аморфные сплавы, получаемые в настоящее время охласдением с максимально возможной скоростью, представляют собой сложные многокомпонентные системы. Даже в наиболее простых бинарных сплавах типа А-В существуют три типа парных корреляций между компонентами: А-А, А-В и В-В.

Для правильного представления структуры аморфных сплавов необходимо провести разделение по всем парным корреляциям тех величин, которые были измерены экспериментально. Интерференционная функция S(Q) двухкомпонентного сплава, определенная в экспериментах по дифракции; равна

5 = а (Q) +2са с в Ьв Sb(Q) + 4 b% Sbb{Q)] (3.20)

где 6л и Ьв-амплитуды когерентного рассеяния атомов АиВ, Са и Св-атомные концентрации компонентов АиВ; <6> = = саЬа + СвЬв-

В выражении (3.20) определенная экспериментально интерференционная функция представлена как суперпозиция парциальных интерференционных функций Saa(Q), Sab(Q) и Sbb(Q) по типам парных корреляций между компонентами: А-А, А-В и В-В. Поэтому, если определить S(Q) трех А-В сплавов одинаковых составов, но с разными величинами Ьа или Ьв, то в принципе можно получить систему трех уравнений, решение которой даст значения парциальных структурных факторов.

Если говорить о рассеянии нейтронов, то здесь наиболее распространенным методом является метод изотопного замещения, посредством которого удается изменить Ьа или Ьв- В этом методе используется то обстоятельство, что соответствующие специальные изотопы CLi, iiCd, iGd и т. д.) дают различное рассеяние. Поскольку эффект различия в рассеянии гораздо более ярко выражен для нейтронов, чем для рентгеновского излучения, то при применении нейтронного рассеяния можно ожидать высокой точности результатов. В частности, на ферромагнитных аморфных сплавах удается разделить парциальные структурные факторы, используя магнитное рассеяние при поляризации нейтронов.

Различие в рассеивающей способности атомов может также использоваться и в случае рентгеновской дифракции. Величины Ьа и Ьв могут изменяться при изменении типа излучения. Поэтому

1 В тексте оригинала сильные различия в рассеивающей способности атомов (т. е. величин Ьа и Ьь), обеспечиваемые изотопным замещением или изменением типа излучения, названы необычным (аномальным) рассеянием. Прим. ред.

3* Зак. 307