Зная разность радиусов Ri - R резца и его осевые размеры, находим профиль инструмента. Высота профиля В = Ri - R. Для точного определения профиля резца в уравнении (2.14) необходимо задаться рядом значений текущих осевых размеров х детали и для каждого из них найти радиус R. Обычные вычисления окажутся слишком трудоемкими, поэтому данную задачу целесообразно решать на ЭВМ, используя формальные языки программирования. Рассмотрим пример программы на языке PUI, реализованного в ДОС ЕС ЭВМ. Преобразуем третье уравнение системы (2.10) к виду, позволяющему находить угол 8 как функцию его тангенса:

0 = arctg

г1 sin Yi

+ Yi-

(2.16)

Введем в формулу (2.16) обозначения: Sf = ri sin Vi; Sa = X tg P; Sa = Sj/Sa, после чего выражения (2.14) и (2.16) примут

= /(Sa Sin Q-fi-Ri cosaif - (Sa cosQ - Ri sin a,

e = arctg(i)+Vx.

(2.17) (2.18)

определим (2.19)

Произведем идентификацию имен вычислительных формул символами алгоритмического языка PL/I.

в ТЕТ

При заданном числе точек п на оси X от дтш ДО Хща шаг Дл; изменения координаты х:

Дл; = JCnax - ХтЛп - I)-

В алгоритме ..... X

В программе...... X

В алгоритме ..... R

В программе ;..... R

Лх DX

1 ALF

Si Si

GAM Sa Ss

Обозначим блок, вычисляющий координаты точек профиля резца, идентификатором PROF и запишем его в таком виде:

PROF:PROCEDURE; GET EDIT (BET. RM, RB, ALF, GAM, A, B) (F (A, 5)); GET EDIT (K) (F (3)); Si = RM * SIN (GM); DX = (B - A)/(K - 1); DO X = A BY DX TO B;

Sa = X * TG (BET); S, = TET = ATAN (SQRT (1 - S3 ** 2)/S3) -f GAM; R = SQRT ((S, * SIN (TET) - RM - RB * COS (ALF) ** 2 -- (Sa * COS (TET) - RB * SIN (ALF)) ** 2);

PUT EDIT (КООРДИНАТА X ,

РАДИУС R) (SKIP, X (15), A, X (15), A);

PUT EDIT (X, R) (SKIP (2), X (15), F (8,6), X (5). F (8, 6);

END; /*ЦИКЛА ПО X */

END; /*PROF */

Определение профиля фасонных резцов геометрическим способом. Как уже отмечалось, этот способ основан на решении простых трехчленных уравнений, широко используемых на практике. Пусть размеры обрабатываемой детали заданы в соответствии с рис. 2.5. С учетом качества обрабатываемого материала по табл. 2.1 выбираем передний угол у. Задний угол принимаем равным 10-12. Для примера рассмотрим методику профилирования круглого фасонного резца. Расчет профиля резца для обработки различных участков детали ведут последовательно от одной базовой точки / или линии 1-1, в которой для неповернутых резцов его вершину устанавливают по высоте центров детали. Расчетная схема строится без масштаба. Для конического участка детали 1-2 она показана на рис. 2.6. Прежде всего определим исходный наружный диаметр Df резца, или радиус R. Для этого рассчитаем диаметр оправки d из условия ее работы на сложное сопротивление. Исходный наружный диаметр резца (2,5 н-З) d. Диаметр оправки принимают из соотношения d w 0,4/, где / - длина обрабатываемой детали. Расчетные диаметры резца и оправки принимаются по приведенному ниже нормальному ряду.

d, мм...... 12 16 20 22 24 28-30 32-36

£), мм...... 30-40 40-50 50-60 60-70 70-80 80-90 90-100

Центр круглого резца выше центра обрабатываемой детали на величину h. Это необходимо, чтобы образовать задний угол у резца: h= Ri sin 1, где - задний угол резца в точке /.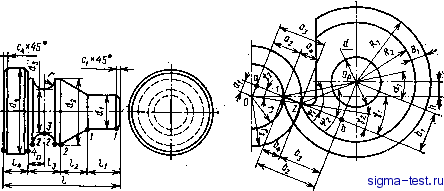

Рис. 2.6. Обрабатываемая деталь

Рнс, 2,6, Схема для расчета профиля фуглого фасонного резца

Методика определения профиля резца следующая. Сначала решают систему прямоугольных треугольников, связанных с обрабатываемой деталью, из которых находят

Ui = ri sin 7i, = fi cos vf, sin = а/г,

аз = Га cos у, a = a - a,

где Yj - передний угол резца в точке 2 его контакта с деталью.

Затем решают систему двух прямоугольных треугольников, связанных с резцом, из которых

bi - Ri sin tj3i, &2 = 1 cos tfi, Ьз = bi~ bi, a &4 = a,

где ifi - угол искажения в точке 1, ifi = Vi -f 1; 2 ~ угол искажения в точке 2, tfa = 72 + 2; tg 2 = i/bs, а% - задний угол резца в точке 2. Тогда искомый радиус резца

/?2 = bifsin 2, (2.20)

а высота профиля резца = Ri - /?2.

Для условных (нереальных) участков 1-3 и /-4 детали (см. рис. 2.5) профиль резца рассчитывают таким же способом. Рассмотренная последовательность решения задачи по определению профиля фасонных резцов однозначно является и алгоритмом программы для расчета на ЭВМ. Определение профиля фасонного резца от одной базовой точки / имеет то преимущество, что при построении расчетных схем для условных участков детали /-5, /-4 и т. д. малый треугольник Oal, связанный с деталью, и большой прямоугольный треугольник OBl, связанный с резцом, остаются неизменными (см. рис. 2.6). Поэтому их размеры определяются только один раз по первой расчетной схеме. Вследствие этого сокращаются вычисления. Кроме того, найденные размеры профиля резца определяются / от этой базовой точки / или линии /-/. Во всех случаях высота профиля резца получается меньше высоты профиля обрабатываемой детали. Анализ приведенных уравнений показывает, что профиль фасонных резцов зависит от параметров обрабатываемой детали и инструмента. Наибольшее влияние на профиль резца оказывает угол конуса детали р, затем передний и задний углы и в меньшей мере размеры резца.

Профиль резца по крайним точкам можно рассчитать только для участков детали, имеющих торцовые уступы. Резцы, рассчитанные таким способом для конических поверхностей, имеют погрешности при обработке. Если передний угол положительный и режущая кромка принимается прямолинейной, то она не будет совпадать с образующей конуса (рис. 2.7), а является наклонной к ней под углом К.

Так как режущая кромка является формообразующей, то обработанная поверхность детали будет не конической, а вогнутой в виде гиперболоида вращения. В результате возникнет погрешность Ai, которую можно устранить, совместив режущую кромку с образующей конуса путем поворота резца на угол к или заточкой его передней поверхности под этим углом. Но так можно делать только для деталей, состоящих из одного конического участка. Для сложного 30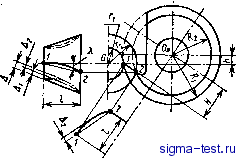

рис. 2.7. Образование погрешностей детали круглым фасонным резцом

контура деталей, имеющих несколько участков, этого сделать нельзя. В более общем случае такая погрешность будет устранена, если для расчета профиля резца взять несколько точек (сечений) на конической поверхности детали. Тогда режущая кромка и профиль резца будут криволинейными - вогнутыми. Однако резцы с криволинейным профилем нетехнологичны. В ряде случаев сложная поверхность круглого резца заменяется более простой - конической, В этом случае режущая кромка резца будет выпуклой, так как она лежит в передней плоскости, которая не проходит через ось резца, а отстоит от нее на расстоянии Я.,В результате возникнет погрешность обработки детали, равная (рис. 2.7). Суммарная погрешность обработки резцом конической формы А = -f Aj. Выпуклость режущей кромки аналитически определена в работе [4 ].

На рис. 2.8 показана схема для решения этой задачи. Находим наибольшее отклонение Ау. Режущая кромка с наибольшей выпуклостью лежит в плоскости передней поверхности резца. Отклонение Ау есть проекция А2 на осевую плоскость резца, определяемое в направлений, перпендикулярном его оси. Запишем уравнение конической поверхности резца

y + z = Р; P = Ri-b,

(2.21)

* Плоскость передней поверхности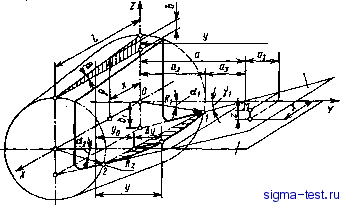

Диаметральная плоскость резца

Рис. 2.8. Определение выпуклости режущей кромки резца

где ft = X tg Р; р - текущий радиус-вектор на конической поверхности резца; - радиус резца в точке /; Р - угол наклона образующей конической поверхности резца.

Уравнение передней плоскости у - а + ai, где а = + Og; fla = Ri cos 1; Аз = Ri sin ajtg y; = г ctg 71.

Таким образом, у - a + z ctgy или

ctgVi

(2.22)

Решив совместно уравнения (2.21) и (2.22), получим квадратное уравнение, которое описывает гиперболическую режущую кромку

- Р >

резца у

2а ± 1А4а- (1 + ctgyi) (а- pctgyi)

(2.23)

2(l+ctg2vi)

Из рис. 2.8 видно, что

а = fti ctg Yi;

bi = Ri (sin 1 + cos a, tg 7). (2.24)

Подставим значение a в уравнение (2.23) и после некоторого преобразования получим окончательное уравнение режущей кромки

резца

y = bi cos 7i sin 7i -f cos 71/ p - b\ cos, (2.25)

где 7i - передний угол резца в точке /.

Уравнение прямой линии, проходящей через крайние точки 1-2 (см. рис. 2.8) режущей кромки,

(2.26)

У1- - {У1-У,

где Ух VI yi - ординаты точек 1 н 2. Из уравнения (2.21) имеем

X = (R, - p)/tg p. (2.27)

Подставив уравнение (2.27) в уравнение (2,26), получим

Величина стрелы выпуклости режущей кромки Ь.у у - у, т. е. Д(/ == fti cos Yi sin 7i -j- cos У1У - ft? cos7i -

(2.29)

, Ri(yi~y2)

-У + -ПiГ~

P (У1 - У2)

/tgp

Максимальная выпуклость получится при значении р, для которого первая производная d (Дг/)/ф = 0.

Дифференцируя уравнение (2.29) и подставив значение bi из (2.24), получим

. Ri {У1 - yi) sin (g + Y) Ртах - ;

\(У1-У2)-1 tg2pcosi>Vi

(2.30)

Haimmei Нсттшег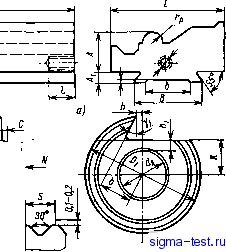

Рнс. 2.9. Призматический (а) н круглый (б) фасонные резцы

Подсчитав по уравнению (2.30) ршах и подставив его в уравнение (2,29), получим максимальную выпуклость режущей Кромки круглого конического резца, который установлен только одной вершинной точкой на высоте центра изделия. Подставив значение ршах

В уравнение (2.27), получим значение абсциссы х, определяющей точку режущей кромки, к которой относится максимальная выпуклость. Исследования, приведенные в работе [4], показали, что наиболее точными являются призматические резцы, у которых прямолинейная режущая кромка совпадает с образующей конуса обрабатываемой детали. В этом случае не возникает погрешность обработки. Это справедливо и для призматических тангенциальных резцов.

Призматические резцы, устанавливаемые только одной точкой режущей кромки по центру обрабатываемой детали, создают незначительную погрешность. Наибольшая погрешность возникает при работе круглыми коническими резцами. Для конических резцов 95 % общей погрешности составляет выпуклость режущей кромки. Детали, обработанные такими резцами, могут иметь вогнутость 0,5-1,5 мм. Задача по определению профиля призматических резцов решается более просто, чем для круглых. Для участка /-2 высота профиля призматического резца = cosijjj (см. рис. 2.6). Для радиусных участков деталей фасонные резцы профилируют по приведенной выше методике. Задаются несколькими точками на радиусном участке детали и находятся также координаты соответствующих точек профиля резца. Расчетный профиль резца получается криволинейным. Для несопряженных радиусных участков с невысокой точностью криволинейный профиль резца заменяют соответствующим радиусом.

2 Иноземцев Г. Г. 33