Рис. 8.21. Образование винтовой поверхности! архимедова червяка

червяк 5 с прямолинейным профилем; в нормальном сечении по витку. Сле-; дует иметь в виду,что корректировать угол профиля легче, чем прогиб. С уче-: том этого червяк 5 предпочтительнее по точности. Конволютные червячные-фрезы изготовляют класса точности В и С для обработки зубчатых колес 9; и 10-й степени точности. При проектировании червячных фрез одним из главных вопросов является определение профиля их зубьев. Вследствие затылования профиль зубьев фрезы будет отличаться от профиля витков исходного червяка. Чтобы найти профиль зубьев фрезы и определить его характеристики, необходимо решить ряд задач в той последовательности, в которой формируется фреза как инструмент, а именно:

1) записать уравнение винтовой поверхности исходного червяка;

2) определить уравнения винтовой поверхности канавки, образующей пространство для размещения стружки и переднюю поверхность;

3) выразить уравнением режущие кромки зубьев фрезы;

4) образовать и записать уравнения боковых затылованных поверхностей зубьев фрезы;

5) найти уравнения профиля зубьев в соответствующем сечении;

6) определить характеристики профиля зубьев фрезы.

Ниже приведено решение этих задач применительно к фрезам, профилируемым на основе исходного архимедова червяка. Методика профилирования эвольвентных и конволютных червячных фрез остается такой же, как и архимедовых.

Уравнение архимедова червяка. Архимедова винтовая поверхность получается в результате винтового движения образующей прямой, лежащей в плоскости осевого сечения XOY относительно оси винта X. Схема образования такой поверхности показана на рис. 8.21:

X - Xi-\- Х2;

Подставив выражения, получим

для левой стороны витка х =6-f р tg а,

для правой стороны витка х = 6 - р tg а

или для правозаходного червяка

=-2-e±ptga.

(8.19)

где 6 - угловой параметр, характеризующий поворот образующей 0/4 относительно оси X в винтовом движении; р - текущий радиус-вектор точки, лежащей на образующей; - шаг винтовой поверхности, Рх = яО tg т; а - угол профиля исходного червяка.

Для левозаходного червяка необходимо поменять знак перед углом 6, т. е. перед первым членом будет (-).

В поперечном сечении червяка, когда л; = О, из уравнения (8.19) получим уравнение архимедовой кривой

2л tga

е = ье.

где b - постоянная, архимедовой кривой.

В осевом сечении плоскостью XOY угол 6 = 0, а р - у. Тогда из уравнения (8.19) х= ±tg аг/. Это есть уравнение образующей прямой.

Уравнение винтовой поверхности канавки. Если передний угол фрезы равен нулю, то образующая канавки - прямая, пересекающая ось X винта под прямым углом. Такая винтовая поверхность - коноид, частный случай архимедовой поверхности. Поэтому уравнение канавки получается сразу же из уравнения (8.19), если принять угол а = 0.

Учитывая, что для правозаходного червяка канавка левозаходная и наоборот, будем иметь

-v =±-g-. (8.20)

где Р - шаг винтовой поверхности канавки, Pi, = nDctg(o. Здесь верхний знак относится к правозаходной канавке, нижний - к левозаходной.

Уравнения режущих кромок. Режущие кромки получаются в результате пересечения поверхности червяка винтовыми канавками. Их уравнения получим в результате совместного решения уравнений указанных поверхностей.

Для этого из уравнения (8.20) находим

е = Т2я

Подставив значение угла б в уравнение (8.19), для правозаходного червяка получим

= --%±lg P или + -±tg p.

к к

Так как поверхности пересекаются по режущим кромкам, для любой точки л; = л; = Хр. Поэтому

( р/ )p =d=tgap; отсюда

tgap.

(8.21)

Здесь верхний знак относится к левой режущей кромке, нижний - к правой. Для левозаходного червяка в уравнении (8.21) необходимо поменять знаки на обратные.

уравнения боковых затылованных поверхностей зубьев фрезы. Затылование зубьев производится с целью создания задних углов по всему контуру. Затылованные поверхности должны удовлетворять двум условиям: проходить через режущие кромки, и их винтовой ход должен отличаться от винтового хода исходного червяка.

Чтобы получить их уравнения, свяжем режущие кромки с подвижной системой координат и сообщим им движения, соответствующие движениям при затыловании. Тогда в общем виде уравнения боковой затылованной поверхности зубьев фрезы запишутся так:

= -Ь 3 = % -Ь Pii%;

в = вр-ье,. ;

Решив совместно эти уравнения, исключим угловой параметр затылования. Из нижнего уравнения

Эз = 0и-ер.

Подставив выражение 63 в верхнее уравнение системы, получим

х = хр + р;,(е -ер), (8.22)

йдесь Хр определяется по уравнению (8.21); Р = Ph/2ii - винтовой параметр затылованной поверхности; 63 - угол поворота режущей кромки в затыловочном движении; 6и - угол, определяющий положение точек на затылованной поверхности; 9р - угол, определяющий первоначальное положение точек режущей кромки до затылования.

Угол Эр находят из совместного решения уравнений (8.19) и (8.20), исключив из них х и х. Так как х = х = Хр, то & = 6р.

Тогда ep±tgap = -ep; илн 6, (-2) = + tgap.

Откуда

tgop.

Подставив это значение Эр в уравнение (8.22), получим

,P;..(Q.±-ptgap)+Xp

г. , Рв 2п . , Рк

Эи±-рггргр±-р;п

tgop;

Ри л , Рк + Ри tp..

(8.23)

где Ри - винтовой ход боковых затылованных поверхностей.

Здесь также верхний знак справедлив для левой боковой затылованной поверхности, нижний - для правой. 174

Для левой стороны Хд = хл а Р = Ра.п- Для правой стороны

Хи = Ха.а> Ри = Ра. п- ТоГДа

X -- и-- й I Рк + Ри.л tcan-

Ри.,

(8.24)

Q Рк +Ри.п

2я Р +Рх Р-

где Р - шаг витков исходного червяка, Р = nD tg т; Р - шаг винтовой стружечной канавки, образующей переднюю поверхность зубьев фрезы. Як = ctg со; Э - угол, определяющий положение точек на затылованных поверхностях; а - угол профиля исходного архимедова червяка; р - текущий радиус-вектор точки, лежащей на боковой затылованной поверхности.

Для левозаходных фрез в уравнениях (8.23) и (8.24) необходимо изменить знак перед 6и на обратный.

Так как винтовой ход боковых затылованных поверхностей и. л и Ри. п отличается от винтового хода исходного червяка, то в общем виде для правозаходных фрез

Р, =Р,-АР\

P.., = P. + SP.

где АР - дополнительное перемещение затылованных поверхностей в осевом направлении фрезы.

На рис. 8.22 показано смещение контуров затылованных поверхностей зубьев за один оборот фрезы. Из рисунка видно,- что

ДЯ = ААх = /С tg а

где /С - величина затылования поверхности на вершине витка за один полный его оборот; - угол профиля затылованного витка, т. е. зубьев фрезы.

Так как затылованные поверхности не совпадают с поверхностями исходного червяка, то Ф а. Для левой стороны зуба и = и. л для правой а = а . Тогда

и.л = P;,-<tga .л; Р..и = Р.Л-КЧа,.п.

(8.26)

Значение К найдем из геометрии и кинематики процесса затылования. Стандартные червячные фрезы делают так, что у них винтовая канавка проходит перпендикулярно к виткам исходного червяка на делительном диаметре. Развертка на плоскость для правозаходной червячной фрезы показана на рис. 8.23. Шаг между зубьями фрезы

Р = ОС + СВ = а ctg со + а tg т = а (ctg со + tg т).

где ctg со =

Тогда Р, = а(- + ). Откуда a=nD

Р + Рх

где а - смещение по дуге окружности одноименных точек О и Л двух режущих кромок, лежащих на одной и той же передней поверхности, но. принадлежащих двум разным виткам зубьев фрезы.

Если канавки прямые, что характерно для фрез сборной конструкции, то угол со = О, тогда и смещение а = 0. Когда будут отзатыло-ваны все зубья данного витка, то, как видно из рис. 8.23, фреза повернется не на полный оборот, т. е. не на nD, а на nD - а. Тогда

nD - а = nD - nD

Рк + Рх

или nD - a = nD

Pr + Px

Рк + Рх

при повороте фрезы на один торцовый шаг радиальное перемещение затыловочного резца или круга равно Кг- За время поворота фрезы на nD - а, радиальное перемещение затыловочного инструмента будет равно Кг- За полный оборот фрезы на nD радиальное движенпе затылования равно К-

Очевидно, что

К яО nD

лО - а

Рк + Рх Рк

Откуда

Рк + Рх Рк + Рх

(8.27)

где Z - число торцовых зубьев фрезы.

Подставив значение К в уравнение (8.26), для правозаходных фрез получим

Рк + Рх Рк

Кг tga .,

(8.28)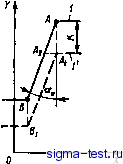

Если канавки прямые, то K=KzZ. Тогда

.л = P;c-Л:ггtga .я; Р.п = Рх + К, 2tga . .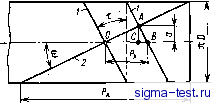

Рис. . 8.22. Смещение конт}в при затыловании:

J - иачальный контур; / - конечный контур

Рис. 8.23. Развертка червячной фрезы на плоскость:

J - след винтовой линии зубьев фрезы; 2 - след винтовой линии окружности канавки 176

Рис. 8.24. Развертка витка исходного червяка и затылованных поверхностей на плоскость для фрез с прямыми (а) и винтовыми (в) канавками:

пунктирная линия - линия витка исходного червяка; сплошная линия - зуб фрезы

Как и следовало ожидать, из этих уравнений видно, что в сечении правозаходных червячных фрез, соосным делительным цилиндром, для левой стороны

зубьев винтовой ход боковых затылованных поверхностей получается меньше винтового хода витков исходного червяка, а для правой стороны зубьев - больше. Для левозаходных червячных фрез будет наоборот..

На рис. 8.24 дана развертка витка червяка и затылованных поверхностей фрезы по делительному цилиндру, на которой показано уменьшение (-АР) и увеличение(+АР) шага затылованных поверхностей для левой и правой стороны зуба на одном полном обороте витка.

Может оказаться, что для правозаходных фрез Р . =0, а Р . = = 2Р. Это зависит от величины заднего угла. Если задний угол на боковых сторонах зубьев в осевом направлении ос будет равен углу подъема т витков исходного червяка, то АР = Р. В этом случае затылованная поверхность с левой стороны получится не винтовой, а кольцевой. Если а,с > т. то для левой стороны зуба боковая затылованная поверхность из правозаходной перейдет в левозаходную. Это свойство может проявляться у червячных фрез повышенной точности или прецизионных, у которых угол подъема винтовой линии т небольшой, до 3°.

В уравнениях (8.28) неизвестными являются только углы профиля зубьев фрезы . л и и.п-

Профиль зубьев фрезы. Профиль зубьев архимедовых червячных фрез определяется в осевом сечении. В сечении боковых затылованных поверхностей осевой плоскостью XOY угол 6 =; О и р = у.

Тогда из системы уравнений (8.24) получим

Рк + Ри. л

Шс(.у; igay.

(8.29)

Рк + Рх Рк + Ри. п Рк + Рх

уравнения (8.29) описывают тоже прямые линии, но с другими углами профиля л и т. е. с другими углами их наклона к оси У. Как следует из рис. 8.21, для исходного червяка tg а = х/у.

Пользуясь уравнениями (8.29), можем определить углы профиля зубьев фрезы в осевом сечении

t . Xn.j, Рк + Ри. л

& и. л -

tga .n =

Ха. п

Рк + Рх Рк + Ри. п Рк + Рх

tga; tga.

(8.30)