Для образования задней затылованной поверхности инструмента сообщим режущей кромке сложное движение затылования, состо ящее из равномерного вращения относительно оси фрезы 2ф и равномерного поступательного перемещения к центру фрезы. В результате таких движений затылованная поверхность Б будет описана со-, вокупностью архимедовых кривых.

Для образования затылованной поверхности с режущей кромкой свяжем подвижную систему координат 5ф (ХфКф2ф). Ось 2ф параллельна оси 2ф неподвижной системы координат 5ф. Вначале ось ¥ф совпадает с осью Кф, а ось Хф параллельна оси ф.

В системе 5ф уравнения (5.16) примут вид

хф = R sin т; Уф = i? cos т - Ri, 4 = 2 . (5.20) Формулы перехода из системы 5ф в систему 5ф будут Хф = хф cos Q + уф sin Q + iRi - Щ sin в;

Уф = хф Sin е + Уф cos 9 + (Ri. - АК) cos 9; (5.21)

С учетом этого уравнения затылованной поверхности зубьев дисковой фасонной фрезы будут

Хф = Ra Sin т COS в -f (Ry, cos т - Ri) sin 9 + - AK) sin 9; Уф = R sin T sin 9 -f (R cos т - R) cos 0 -f (i?i - AK) cos 9;

(5.22)

2ф = гф - .-arcs, ( i2X)-v..

Здесь угловой параметр затылования изменяется от 9 = О до 9 = Oj,; 9 = 3607г (z - число зубьев фрезы).

Приближение затылованной поверхности по архимедовой кривой к центру фрезы на АК соответствует повороту фрезы при затылова-нии на угол 9. Если 9 = 9, то АК = Кг, где К - полный подъем затыловочного кулачка, соответствующий повороту фрезы при за-тылованин на центральный угол 9 между зубьями.

Профиль зубьев фрезы определяется в осевой плоскости ХфУф, когда Уф = 0. Уравнения профиля следующие:

Хф = R sin т cos 9 + {R cos x - R) sin 9 -f (/?i - AK) sin 9;

(5.23)

2ф = 2h = -У sin a -b г cos 9 + В cos 9. При Уф = 0 из уравнения (5.22) будем иметь Ra Sin т sin 9 + (R cos т - R) cos 9 + (/?i - Д/С) cos 9 = 0. (5.24)

Угол X определяется по уравнению (5.19), а радиус R по уравнению (5.17).

Как видно из рис. 5.23, режущая кромка принадлежит трем поверхностям: передней, исходной и затылованной. Любая точка 106

на режущей кромке одновременно лежит на исходной поверхности вращения и на затылованной поверхности. Поэтому для любой точки режущей кромки т = 9.

Для решения системы уравнений (5.23) задаемся рядом значений .гф = 2 . Из уравнения (5.13) определяем соответствующие х и уц. Затем по уравнению (5.17) находим ряд значений R , подставляя которые в уравнение (5.23) находим Хф. Численное решение такой задачи является трудоемким. Для решения подобных задач целесообразно составлять программу для расчета на ЭВМ.

На основе изложенного выше математического описания алгоритм профилирования дисковой фасонной фрезы в операторной форме может быть представлен в следующем виде.

1. Присвоить значения исходным параметрам D, ц>, а, , yj, л, т, Хо = А, Уо = О, 2о = В. Принять шаг наращивания переменной / (Д/ = 1 мм).

2. Вычислить t = nDctgco; Р = = а tg фс. к = R sin ф; /о х; /о &; /о г по формулам (5.9). Присвоить / = / , здесь / и / - начальная и конечная точки главной режущей кромки.

3. Решить уравнение (5.10) с учетом (5.5), (5.7), (5.8), (5.9) относительно ф на отрезке О < ф <: с точностью е = 0,-0001 мм,

6i = 0,00001 рад.

4. Если нет решения, то / = 7 -f AI, и идти к п. 3, пока / <;

< /к-

5. Вычислить Хи, у , 2i, по (5.13); /? по (5.17).

6. Печатать 2 ,

7. Вычислить т по (5.19).

8. Принять 9 = 0.

9. Вычислить Хф, Уф по (5.21);/?ф = у4 + у .

10. Печатать /, 2 и Рф. Если / < /, то продолжить вычисления по п. 3.

В п. 3 уравнение (5.10) является трансцендентным. Для решения этого уравнения на современных вычислительных машинах можно использовать стандартную подпрограмму RTMI, входящую в математическое обеспечение машины ЕС.

Итерационный процесс решения уравнения (5.10) можно осуществить иначе, методом деления отрезка пополам. Для этого уравнение (5.10) рассматривается как функция неизвестного ф. Задаются - интервалом изменения независимого переменного фц < ф <: if и величинами е и Ej, регулирующими точность решения. Вычисляют значения / (ф) = О на концах интервала и ф. Знаки полученных значений должны быть разными. В этом случае значение функции вычисляется в середине интервала, затем продолжается такое решение в полуинтервале, на концах которого функция имеет разные знаки.

Блок-схема алгоритма решения трансцендентного уравнения (5.10) методом деления интервала пополам показана на рис. 5.26.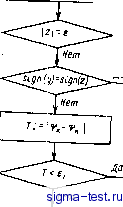

Печатать Нет решения -

Решение найдено

y:=fM

Mem >-r Да

Ь:=р

Tifern

Печатать .Точность исчерпана )

Рис. 5.26. Блок-схема алгоритма решения уравнения (5.10)

Как было показано ранее и как видно из рис. 5.25, высота профиля зубьев фрезы уменьшается по сравнению с высотой профиля исходной поверхности, если передний угол положительный.

Аналогично определяется и профиль фрезы для другой части канавки спинки. Профиль фрезы получается криволинейным, не-технологичньш. Поэтому расчетный профиль фрезы заменяют более простым, показанным на рис. 5.27. Он описывается тремя или двумя плавно сопряженными дугами окружностей радиусов п и гг и прямой линией под углом ф = 10-f-15°, обращенной к спинке канавки. 108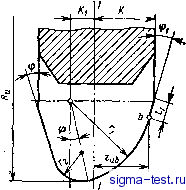

Рис. 5.27. Профиль дисковой 4фезы:

j-}m- осевая лииия, лежащая в плоскости фрезы, которая проходит через точку скрещивания осей фрезы и сверла

На рис. 5.27 положение оси 1-1 вполне определенно и фиксируется размером К от базового торца фрезы:

К = г ь+ к sin Ф1,

где - аппликата, соответствующая крайней точке Ь контакта режущей кромки фрезы с наружным диаметром сверла; 1 - дополнительный прямол-инейный участок режущей кромки, который принимают 2-4 мм в зависимости от диаметра сверла. Прямая длиной проводится по касательной к окружности радиуса ri в точке b под углом ф1.

Межосевое расстояние (см. рис. 5.20) А = -f а, где а - радиус сердцевины сверла. Угол скрещивания осей фрезы и сверла а = 90° - (О - (1 -ь4)°, т. е. фреза устанавливается не по направлению канавки, а на 1-4° меньше. Это делается для того, чтобы исключить или уменьшить вероятность подрезания профрезерованной поверхности канавки.

Профиль фрезы также зависит от ее диаметра, поэтому перед профилированием должен быть определен диаметр фрезы; ориентировочно его можно принимать Z) = 1)ф = 13 j/D, гдеП - диаметр сверла. Диаметр отверстия под оправку d = (0,3-0,4) йф; здесь меньший коэффициент относится к большим диаметрам фрезы. Найденные и d округляются до ближайших размеров по нормальному ряду диаметров. Число зубьев фрезы г = 18-14, причем с увеличением диаметра z уменьшается.

Если винтовую поверхность канавки на инструментах или на других деталях можно выразить одним уравнением, то задача профилирования дисковой фрезы для формообразования заданной канавки решается по рассмотренной методике не по участкам, а в целом для всей поверхности.

Определение профиля дискового абразивного круга для шлифования заданной винтовой поверхности канавки производится так же, как и для дисковой фрезы, только решение задачи несколько упрощается. Оно заканчивается на этапе нахождения исходной поверхности и ее сечения осевой плоскостью инструмента.

глава

ИНСТРУМЕНТЫ для ИЗГОТОВЛЕНИЯ РЕЗЬБЫ

Резьба в машиностроении имеет самое широкое распространение как для крепежных изделий, так и для механизмов, передающих движение (ходовые винты и гайки к ним в станках). Резьба является сложной винтовой поверхностью, к которой предъявляются высокие требования по точности и чистоте обработки. Формообразование резьбы является сложным процессом. Вследствие этого резьбовые инструменты работают в очень трудных условиях.

Образование резьбы производится методом резания и методом пластической деформации. По первому методу работают резьбовые резцы, гребенки, резьбовые фрезы, метчики, плашки, резьбонарезные головки, резьбовые шлифовальные круги. По второму методу работают резьбонакатные ролики и плашки для образования наружных резьб и бесстружечные метчики для изготовления внутренних резьб.

РЕЗЬБОВЫЕ РЕЗЦЫ И ГРЕБЕНКИ

Резьбовые резцы нарезают резьбу за несколько рабочих ходов (проходов). Производительность резьбонарезания низкая. Вследствие этого их в основном применяют в единичном и мелкосерийном производстве для изготовления как наружных, так и внутренних резьб значительной длины или же большого диаметра.

При нарезании резЬбы резец относительно детали совершает винтовое движение с заданным параметром резьбы. Обычно деталь вращается вокруг своей оси, а резец равномерно перемещается вдоль оси детали и за каждый рабочий ход имеет радиальное врезание. Окончательно резьба формируется на последнем рабочем ходу, когда режущие кромки лежат на заданной винтовой поверхности.

Резьбовые резцы бывают стержневые, призматические и круглые. Призматические и круглые резцы рассчитывают и устанавливают относительно детали так же, как и фасонные резцы.

Для уменьшения числа рабочих ходов и повышения производительности труда применяют резьбовые гребенки. Их используют для изготовления крепежной и другой резьбы с мелким шагом.

Рабочая часть гребенки имеет 6-8 шагов резьбы. Из них 1,5- 2 шага расположены на режущей части и 4,5-6 шагов - на калибрующей части (рис. 6.1). При нарезании резьбы напроход на режущей части может быть 3-4 шага. Вершины зубчиков на режущей части срезаны, образуя заборный конус с углом ф = 25-ь30°, благодаря чему срезаемый припуск и работа резания распределяются между несколькими режущими кромками. Вследствие этого на-110

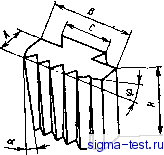Рис. 6.1. Элементы рабочей части резьбовой 1ребеики

Рнс. 6.2. Призматическая резьбовая гребенка

грузка на каждую режущую кромку уменьшается и увеличивается стойкость инструмента. Число рабочих ходов при нарезании резьбы гребенками уменьшается в 2-3 раза по сравнению с резьбовыми резцами. При каждом рабочем ходе гребенка радиально врезается в заготовку и за каждый ее оборот перемещается на один шаг вдоль оси заготовки.

Резьбовые гребенки подразделяют на призматические и круглые - для наружной и внутренней резьбы. На рис. 6.2 показана призматическая гребенка. Как правило, их делают с нулевым передним углом и устанавливают передней поверхностью в осевой плоскости детали.

На практике получили более широкое применение круглые гребенки, как более простые в изготовлении и допускающие большое число переточек. Круглые гребенки обычно делают насадными. Их конструктивные размеры определяются так же, как и фасонных резцов. Круглые гребенки бывают с кольцевыми витками и винтовыми (рис. 6.3). При установке центр гребенки превышает центр детали на величину h для образования заднего угла а. Для уменьшения искажения профиля передний угол у круглых гребенок обычно равен нулю. Ось гребенки с кольцевыми витками может рас-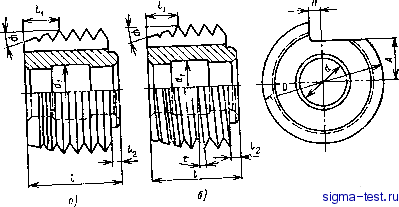

Рис 6.3. Круглые резьбовые гребенки: J с кольцевыми витками; б - виитовая