

 |
 |
|
|
Навигация
Популярное
|
Публикации «Сигма-Тест» Проектирование металлорежущих инструментов 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 [ 16 ] 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 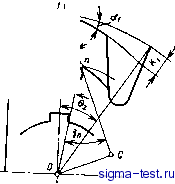 Рис. 5.20. Определение профиля фрезы су >0 где Лд -. высота или глубина профиля канавки детали, которая задана чертежом. Для определения необходимой высоты профиля зуба фрезы надо найти hф. Из рис. 5.20 А/1ф =i е . Кг = Qz-Отсюда кф = !. Учитывая, что Аг = -tgaj АЛ*: и й 360° получим лРВп 360= Найдем угол е . Из треугольника 01п видно, что угол 9 = -Уп - Yi- Передним углом в точке / задаются в пределах 10-20° Передний угол в точке п найдем из соотношения siпY ==-£- = Rh, здесь где ОС = Hi sin у. Тогда sinY = rzsinYi, где Ri - наибольший радиус фрезы в точке 1; R R - текущий радиус точки режущей кромки. Отсюда видно, что при приближении точек режущей кромки к центру фрезы передний угол для них увеличивается. Осевые размеры профиля не изменяются. Поэтому с увеличением высоты профиля зубьев фрезы будет изменяться вид кривой и, в частности, углы профиля. На рис. 5.21 показаны совмещенные профили детали (сплошная линия) и корригированный (расчетный) профиль фрезы (пунктирная линия). Вследствие влияния переднего и заднего углов высота профиля зубьев фрезы становится меньше. Осевые размеры профиля зубьев фрезы и детали остаются одинаковыми. Если профиль детали очерчен прямыми линиями (рис. 5.21, а), то высоту профиля зубьев фрезы рассчитывают по двум крайним точкам. На рис. 5.21, а они обозначены 1 и п. Если же профиль детали криволинейный (рис. 5.21,6), то между крайними точками Inn профиля изделия необходимо принять еще несколько промежуточных точек 2, 3, 4.,. Число Рис. 6.21. Совмещенные профили детали и фрезы 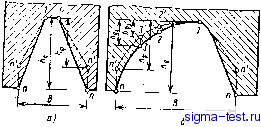 рромежуточных точек принимается в зависимости от вида кривой профиля. Тогда для профиля зуба фрезы получим соответственно расчетные точки 2, 3, 4... Чем больше взято расчетных точек, тем плавнее будет кривая, проведенная через них. Кривая профиля зуба фрезы будет отличаться от кривой профиля- изделия. Расчетная кривая профиля зубьев фрезы может аппроксимироваться другой более технологичной -кривой. Профилирование дисковых фасонных фрез для обработки винтовых канавок. При обработке поверхностей винтовых канавок про(})иль исходной поверхности инструмента и профиль зубьев фрезы, имеющий передний угол равным нулю, отличаются от профиля таких канавок. Объясняется это тем, что винтовые канавки дисковыми инструментами (фрезами и шлифовальными кругами) обрабатывают методом бесцентройдного огибания. При этом нет начальных окружностей, по которым изделие и инструмент в относительном движении формообразования катятся без скольжения, но поверхность канавки образуется в относительном движении в результате ряда последовательных резов режущими кромками различных зубьев в разном их положении. В процессе образования винтовых канавок обычно заготовка имеет два равномерных движения: вращательное относительно своей оси и поступательное вдоль оси, т. е, совершает винтовое движение с заданным винтовым параметром Р = s/2n. Фреза равномерно вращается относительно своей оси с принятой скоростью v. Касание точек режущих кромок фрезы с поверхностью канавки происходит по пространственной кривой, называемой контактной линией, или характеристикой. Сообщив характеристике круговое движение относительно оси фрезы, получим исходную поверхность инструмента. Сообщая характеристике винтовое движение с параметром Р в системе детали, получим поверхность винтовой канавки. Для определения профиля зубьев дисковой фрезы должны быть заданы форма и размеры профиля винтовой канавки, угол о между осями заготовки и фрезы и расстояние между осями А. Профиль канавки обычно задается в торцовом сечении изделия или в нормальном сечении к винтовой канавке. Профиль канавки может быть задан и в другом сечении. Угол между осями фрезы и изделия а = 90°- о> - (14)°, где О) - угол наклона винтовой канавки к оси изделия по наружному диаметру. Рассмотрим решение поставленной задачи для поверхности канавки сверла, образованной прямолинейной режущей кромкой. Пусть все необходимые параметры сверла, показанные на рис. 5.22, являются заданными. Сверло при обработке винтовой канавки вращается с равномерной угловой скоростью со и движется в осевом направлении со скоростью Ра>, где Р - параметр винтовой поверхности канавки сверла. На рис. 5.23 показаны принятые системы ортогональных координат. 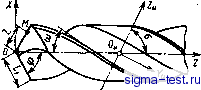 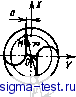 Рис. 5.22. К определению профиля дисковой фрезы для винтовых каиавок Запишем уравнение главной режущ,ей кромки в начальном положении. В этом положении системы S и Sp совпадают. Координаты любой точки М на режущей кромке сверла в системе XpVpZp Хр = I sin ф; Ур = -а; 2р = / cos ф, (5.3) где I - длина режущей кромки до точки М, I - R cos р; здесь R - текущий радиус точки режущей крсшки сверла; л - угол наклона режущей кромки в данной точке. Сообщив режущей кромке винтовое движение относительно оси сверла Z, получим часть винтовой поверхности канавки, образу-. ющую переднюю грань. Для этого свяжем с режущей кромкой подвижную систему координат и сообщим ей указанное винтовое движение относительно неподвижной системы S. Формулы перехода от системы Sp к системе S следующие: X = Хр cos \р - Ур sin ij); у = Хр sinij) -f Ур cos \з; (5.4) 2 = 2р -Ь Pijj. Подставив из системы (5.3) значения Хр, Ур и 2р в систему (5.4), получим уравнения винтовой передней поверхности сверла X = / sin ф cos ij3 -Ь а sin \jj; у = / sin ф sin If - а COS tf; (5.5) 2 = / COS ф Ч- РМр, где \j) - угол поворота системы Sp относительно системы S; Р - параметр винтовой поверхности канавки. Шаг винтовой поверхности канавки t = nD ctg (О, где (В - угол наклона винтовой канавки к оси сверла. Рис. 5,23. Принятые системы координат: S (XYZ) - неподвижная система, связанная со сверлом; Sp (JCpVpZp) - подвижная система, связанная с режущей кромкой сверла; S (X y Z ) - система, связанная с дисковой фрезой 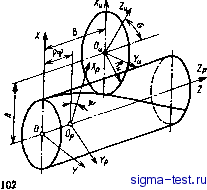 Поместим дисковую фрезу в канавку сверла, направив ось Уи вдоль канавки, а ось фрезы под углом а к оси сверла (см. рис. 5.22 и 5.23). В процессе формообразования нормали к поверхности канавки и фрезы в точках их контакта будут общими. В общем виде нормаль к поверхности F = F{1, -ф) запишем так: iV = -5rXg. (5.6) Для определения частных производных в выражении (5.6) продифференцируем уравнения (5.5) dxidl = sin ф cos \jj; dyldl = sin ф sin tjj; dzldl - cos ф; dxld = -/ sin Ф sin ф -f a cos \J5; dyld = ; sin Ф cos \3 -f a sin if; a2/a\) = p. Подставив полученные значения частных производных в формулу (5.6), будем иметь - sin ф sin vfP - cos ф (/ sin ф cos ф -f a sin ф); Ny - cos Ф (-/ sin Ф sin ij) + a cos ф) - sin ф cos P\ N. = sin Ф cos \3 {I sin Ф cos \) -f -f a sin ф) - sin Ф sin ф (-I sin ф sin vf -f a cos ф). После некоторого преобразования компоненты нормали будут следующими: - sin фР - ctg ф {I sin ф cos ф -h а sin ф); -cos 1?Р - ctg ф {I sin ф sin ф - а cos ф); N~ = I sin ф. Дисковая фреза является телом вращения, поэтому нормаль в точке касания поверхностей фрезы и канавки будет пересекать ось фрезы. Координаты точки 0 в системе S: = Л; Уо, = 0; 2о = В. (5.8) Возьмем на оси фрезы единичный вектор Iq. Проекции его на оси координат в системе S сверла будут 1ош = 0; /ohj, = - sin а; /оиг = cos о. (5.9) Условие пересечения нормали к винтовой поверхности и вектора /о (оси фрезы) имеет вид х-Хо,у-уог- 2о,. М. N, 1 = 0 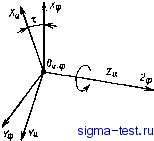 (5.11) Рис. 5.24. Расположение систем координат Sb, > ~iy-yo )iNJo z-lo..N,)i- + (z - 2ои) (iVJo . - lo .N,) = 0. (5.10) В уравнении (5.10) координаты соответствующих точек определяются по уравнениям (5.5)-(5.9). Совокупность точек касания, через которые проходят нормали к сопряженным поверхностям, описываемых уравнением (5.10), есть характеристика, т. е. контактная линия в координатной системе S, связанной со сверлом. Для определения профиля зубьев фасонной дисковой фрезы запишем характеристику в системе Sy, (Х Ки2 ), связанной с фрезой. Для этого воспользуемся матричным равенством z ~ = г 1 1 где Ми. с - матрица, связывающая системы и S. Из рис. 5.23 видно, что матрица 1 О О -А О -- cos о + sin о в sin о I О - sin о + cos о В cos о 0 0 О 1 Раскрывая матричное равенство (5.11) подстановкой в него выражения (5.12), получим уравнения характеристики, записанные Б системе фрезы: Хи = X - А; г/и = г/ cos а + Z sin о -f В sin о; (5.13) ?h = - г/ sin а + Z cos а -t- в cos а, где X, у, г определяются из уравнения (5.5); А - расстояние между осями сверла и фрезы; В - расстояние между началом координатных систем 5и и S в направлении оси Z; а - угол скрещивания осей сверла и фрезы. Для образования исходной поверхности дискового фасонного инструмента сообщим характеристике круговое движение относительно оси фрезы. Для записи уравнения искомой круговой поверхности введем условно неподвижную систему координат 5ф, в которой будет поворачиваться система S вместе с характеристикой. Координатные системы расположены так, как показано на рис. 5.24. Оси Zh и 1ф совпадают. (5.12) 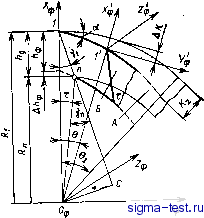 Рис. 6.25. Образование режущей кромки и затылованной поверхности зубьев фрезы: А - исходная поверхность; Б - заты-лованная поверхность Формулы перехода систем координат от системы 5я в 5ф Хф = х cos г - у sin т; = j: sin т-- cost; (5.14) 2ф - 2и. Подставив в (15.14) значения jCh. Уи и 2и из уравнений (5.13), получим уравнения исходной поверхности фрезы Хф = (х ~ А) cos х ~ (у cos о Н- 2 sin о + В sin а) sin т; Уф = (х - А) sin т Ч- (I/ cos о + 2 sin о -f В sin а) cos т; (5.15) 2ф = -У sin а Ч- 2 cos а -f В cos а. Здесь X, у к г находятся также из уравнения (5.5). Учитывая, что каждая точка характеристики определяется радиусом R , а исходная поверхность образуется вращением характеристики, исходную поверхность инструмента можно записать = sin т; Уф = R cos т; гф = 2 , (5.16) где /?и - текущий радиус точки характеристики; т - угол поворота системы S вместе с характеристикой относительно неподвижной системы 8ф, связанной с фрезой (см. рис. 5.24); г - текущее значение аппликаты 2ф, в плоскости которой находится R : /?и = /4+?и, (5.17) где х , г/и определяют по уравнениям (5.13). Для образования режущей кромки зуба фрезы пересечем ее исходную поверхность, определяемую системой уравнения (5.16), плоскостью передней грани 1 - С (рис. 5.25), которая образует положительный передний угол у, в точке зуба, лежащей на наибольшем радиусе фрезы Уравнение передней поверхности Xф(R -Уф)igУl, (5.1?) 2ф = 2п. Подставив (5.16) в (5.18) и произведя некоторые преобразования, получим связь между углом т и радиусом Rj, . = arcsln()-V. (5.19) Уравнения (5.16) и (5.19) описывают режущую кромку зубьев фрезы.
|
|||||||||||||
|
© 2010 www.sigma-test.ru Санкт-Петербург: +7 (812) 265-34-48, +7 (812) 567-94-10
Разработка и поддержка сайта: +7(495)795-01-39 после гудка 148651, sigma-test.ru(my_love_dog)r01-service.ru Копирование текстовой и графической информации разрешено при наличии ссылки. |