Отношение угловых скоростей пары цилиндрических зубчатых колес с параллельными осями обратно пропорционально их начальным радиусам (начальным диаметрам).

Когда контактирующие поверхности начальных окружностей заменяются зубьями, то эти зубья должны располагаться так, чтобы независимо от того, входят ли зубья в зацепление или выходят из него, должны сохраняться постоянные угловые скорости, а следовательно, и передаточное отношение пары. Чтобы удовлетворить эти требования перпендикуляры в точке касания сопряженных зубьев должны всегда проходить через точку касани? начальных окружностей (полюс зацепления), которая находится на линии центров. Профили зубьев зубчатой передачи, которые отвечают этим требованиям, сопрялсеиы друг с другом и с производящей рейкой. Для упрощения расчета введено понятие о делительном диаметре. Модуль и угол зацепления на делительном диаметре соответственно равны модулю и углу зацепления режущего инструмента, которым нарезают зубья-колеса. Делительный диаметр d пропорционален модулю и числу зубьев. Для прямозубых колес делительный диаметр d = mz, для косозубых колес

d = - Диаметр основной окружности di равен произведению

делительного диаметра на косинус угла зацепления:

db = d cos а.

У сопряженной пары некорригированных зубчатых колес, работающих при правильном межосевом расстоянии, начальные окружности совпадают с делительными окружностями

Линией зацепления называют общую касательную EiE (рис. 21) к двум основным окружностям, которая проходит через полюс зацепления Р. По линии зацепления ЕЕ перемещается точка касания двух эвольвентных профилей сопряженной пары зубчатых колес. Когда две эвольвенты совмещены как профили зубьев сопряженных колес и соприкасаются в полюсе зацепления, то все контактные взаимодействия и взаимодействия зубьев происходят вдоль линии зацепления. Если один элемент (шестерня) вращается, то эвольвенты профилей зубьев скользят друг по другу и приводят в движение другой элемент (колесо), вращающийся в противоположном направлении.

Длиной зацепления называют отрезок линии зацепления, заключенный между началом и концом зацепления сопряженных профилей зубьев, т. е. отрезок между точками Q и Cj.

Коэффициент перекрытия является одним из основных факторов, характеризующих конструкцию зубчатых колес. Он определяет продолжительность зацепления зубьев, т. е. число пар зубьев шестерни и колеса, одновременно находящихся в зацеплении. С увеличением коэффициента перекрытия возрастает плавность и прочность зубьев цилиндрической передачи. У цилиндри-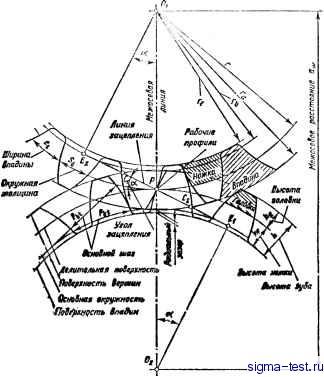

Рис. 21. Внешнее зацепление цилиндрических колее

ческих зубчатых колес различают коэффициенты торцового и ос >-вого перекрытия.

Коэффициентом торцового перекрытия е называют отношение длины зацепления к основному шагуз

Для получения непрерывного зацепления зубчатых колсо иеобходпмо, чтобы длина зацепления была всегда больше, чем Основной шаг. Из трех одинаковых по размеру зубчатых передач (внешнего зацепления, внутреннего зацепления и реечной псрз-дачи) самый маленький коэффициент торцового перекрытия у передач внешнего зацепления, самый большой у передач внутреннего вацепления

Коэффициент осевого перекрытия ер имеет место в шевронных и цилиндрических передачах с косыми и круговыми зубьями. Он дополняет коэффициент торцового перекрытия и зависит от ширины зубчатого венца и угла наклона линии зуба.

Рис. 22. Осевой коэффициент перекрытия:

о - KOCOJyOoe колесо; б - колесо с круговыми зубьимн

Коэффициент осевого перекрытия для косозубых (рис. 22, а)

для колес с круговыми зубьями (рис. 22, t,i--

колес

Контактной линией называют линию на боковой поверхности зуба зубчатого колеса передачи, по которой в данный момент могут соприкасаться сопряженные зубья.

Линией центров называют линию, которая соединяет центры двух сопряженных зубчатых колес (рис. 23). Расстояние между центрами Oi и Ог - межосевое расстояние а,.

Полюсом зацепления Р называют точку пересечения линии центров и линии зацепления.

Углом зацепления а называют угол между линией зацепления и перпендикуляром к линии центров (см. рис. 23). Когда два зуба зубчатых колес с эвольвентным профилем соприкасаются в полюсе зацепления Р, то угол зацепления а у колес будет одинаковым. Одно зубчатое колесо не имеет угла зацепления до тех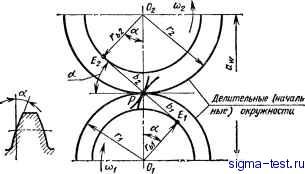

Рис. 23. Взаимодействие двух эвольвент