Общая норма/lb

Рис. 14. Общая нормаль эвольвентных зубьев в точке зацепления

Начальные окрушости

описываемая точкой окружности, катящейся без скольжения по прямой линии). Общей нормалью зубчатых колес с циклоидальным профилем зуба является кривая. Для нормальной работы передачи расстояние между осями сопряженных зубчатых колес должно выдерживаться в пределах жестких допусков. Этот вид зацепления применяют главным образом для мелкомодульных колес в приборостроении.

Эвольвентное зацепление - с профилем зуба, выполненного по эвольвентной кривой. Эвольвентная кривая описывается точкой на прямой РЕ при перекатывании ее по периферии круга (рис. 15). Окружность, по которой перекатывается прямая РЕ, называют основной окружностью.

Эвольвента развертывается из первоначальной точки А на основной окружности радиуса Прямая РЕ, получившая название производящей прямой, касательна к основной окружности в точке Е и перпендикулярна к эвольвенте в точке Р. Отрезок РЕ является радиусом кривизны эвольвенты в точке Р и равен длине дуги АЕ. Угол ф называют углом развернутости эвольвенты Б точке Р.

Угол 6 и радиус-вектор R являются координатами точки Р на эвольвенте. Угол 6 задается в радианах; он является эвольвентной функцией угла зацепления и широко применяется в расчетах зубчатых колес.

Радиан - центральный угол, охватываемый дугой окружности, длина которой равна радиусу этой окружности.

Радиан равен

360° 2я

= 57° 17 46 . Производящая прямая РЕ

определяется из прямоугольного треугольника ОЕР: РЕ = Гъ tg а,.

Угол поворота 6 радиуса-вектора можно определить (в рад) по формуле

6 = inv = tg cix - о-х,

где inv ах = tg а - - эвольвентная функция (инвалюта) угла а для определения которой имеются специальные таблицы; - значения угла давления, град.

Рис. 15. Образование эвольвенты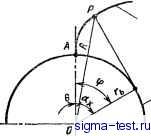

ЭВольВеита

е Осиобмая окружность

Значения эвольвентной функции также могут быть определены (в рад):

Величина радиуса-вектор а R определяется из треугольника ОЕР:

cos а

Радиус кривизны эвольвенты является переменной величиной, в любой точке эвольвенты он соответствует длине производящей прямой, которая определяется по формуле

Цилиндрические зубчатые колеса с эвольвентным профилем удовлетворяют всем современным требованиям плавного и точного вращения, имеется также широкая возможность геометрической модификации профиля. Зубчатые колеса этого типа имеют следующие основные преимущества.

1. Простота формы и возможность высокой точности изготовления режущего инструмента, имеющего реечный профиль.

2. Возможность корригирования эвольвентных зубчатых колес с использованием стандартного зуборезного инструмента.

3. Незначительная чувствительность эвольвентных зубчатых колес к изменению межосевого расстояния.

4. Возможность применения точных и надежных методов контроля эвольвентных зубчатых колес.

Эвольвентный профиль применяют почти для всех зубчатых колес, за исключением зубчатых колес в часовой промышленности, поэтому последующее рассмотрение будет касаться в основном цилиндрических зубчатых колес с эвольвентным зацеплением.

Передача с зацеплением Новикова (рис. 16) в нормальном сечении имеет профили зубьев, выполненные в форме дуг окружностей. Вследствие отсутствия достаточного перекрытия по высоте зубьев зубчатые колеса с этой формой зуба могут быть только косо-зубыми, плавность их вращения зависит от коэффициента осевого перекрытия зубьев колес. Иногда эти условия вызывают ограничения по ширине зубчатого венца. Передачи Новикова обладают большой нагрузочной способностью и износостойкостью, благодаря чему они нашли применение в тяжелонагруженных машинах и механиз- р с. le. Передача с мах. зацеплением Новикова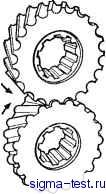

Pi:c, 17. Исходный контур:

в - щишидрических колес внешнего и внутреннего бацвплення; 6 - мо-дифицированный профиль; < - аи яиндрических колес передач Н#ви- ,

кова

Делатель пая пррмал

Р =Ж-т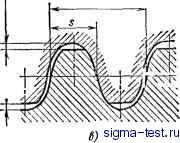

ИСХОДНЫЙ контур, у f 1 ЖЖ-Щ-У зубчатого колеса с беско-нечно большим делительным диаметром эвольвент- t-q ные профили зубьев превращаются в зубья с прямолинейным профилем, они образуют зубчатую рейку. Зуб рейки имеет такие же свойства, как и зуб колеса с эвольвентным профилем. На этом принципе основана широко применяемая передача зубчатого колеса с рейкой. Основные параметры вуба исходного контура рейки определяют параметры проектируемого зубчатого колеса. Если зубчатое колесо с эвольвентным профилем спроектировано с теми же параметрами, что и исходная рейка, то оно будет свободно обкатываться как с исходной рейкой, так и с любым другим зубчатым колесом, спроектированным по одной и той же системе. По этой причине в основу проектирования зубчатых колес и зуборезного инструмента для формирования зубьев колеса методом обкатывания (в беззазорном зацеплении) положен исходный контур.

Исходным контуром называют контур зубчатой рейки с прямолинейным профилем зубьев. По ГОСТ 13755-81 исходный контур для цилиндрических колес внешнего и внутреннего зацепления представляет собой зубчатую рейку с прямолинейным профилем и глубиной захода /г., = 2т (рис. 17, а). Под глубиной захода понимают высоту зуба, которая участвует в работе. Угол профиля исходного контура ад = 20°. Нормальная величина радиального зазора равна с = 0,25т, а радиус закругления у корня зуба исходного контура составляет /- = 0,40т,