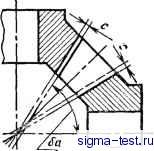Рис. БО. Образование конуса вершин: с - радиальный зазор

которые катятся друг по другу без скольжения, являются воображаемыми. Отношение угловых скоростей пары конических колес обратно пропорционально отношению синусов углов их начальных конусов: ft £1 sin ,\ t

W] r.2 ~ Sill 6 ,2

Понятие начальные конусы относится к конической передаче, отдельно рассматриваемое колесо угла начального конуса не имеет.

Угол делительного конуса б (см. рис. 42) - это угол между осью конического колеса и образующей его делительного конуса. Делительный конус представляет собой коническую поверхность, которая в процессе нарезают зубьев на заготовке катится без скольжения по конической поверхности воображаемого производящего колеса. В некорригнрованных передачах угол начального конуса совпадает с углом делительного конуса.

Угол конуса вершин б (см. рис. 42) - это угол между осью конического колеса и образуюи1,ей его конуса вершчш. Поверхность конуса вершин определяет форму заготовки конического колеса. Для получения постоянного радиального зазора по всей длине зуба в современных методах расчета параметров зубьев конических колес образующая конуса вершин проходит параллельно образующей конуса впадин сопряженного зубчатого колеса (рис. 50).

Угол конуса вершин равен сумме углов делительного конуса и ножки зуба сопряженного колеса;

6 , = + 0,; = +

Угол конуса впадин bj (см. рис. 42) - это угол между осью конического колеса и образующей его конуса впадин. Угол конуса впадин указывают в чертеже, его используют для установки заготовки на зуборезном станке при нарезании зубьев.

Угол делительного дополнительного конуса - это угол между осью конического колеса и образующей дополнительного конуса R, которая перпендикулярна образующей делительного конуса Rf (см. рнс. 42).

Угол головки зуба G (см. рис. 42) - это угол между образующими конуса вершин и делительного конуса.

Угол ножки зуба 6 (см. рис. 42) - это угол между образующими делительного конуса и конуса впадин.

Конусное расстояние R (см. рис. 42) - это длина отрезка образующей делительного конуса от его вершины до пересечения

с образующей делительного дополнительного конуса. Различают внешнее R, среднее Rm, внутреннее Ri и другие Rx конусные расстояния в любой точке ширины зубчатого венца. Конусные расстояния используют при расчете угла наклона линии зуба и развода резцов на внешнем и внутреннем торцах зубчатого венца.

Диаметры конического зубчатого колеса (см. рис. 42). Различают диаметры: внешний делительный d, внешний вершин зубьев dae, внсшний впадин зубьев df и другие диаметры колеса. Внешний диаметр вершин зубьев конического колеса - теоретический (расчетный) размер заготовки. Практически этот диаметр меньше благодаря снятию фаски или округлению вершин зубьев на внешнем диаметре.

Высота зуба h (см. рис. 42) - расстояние между окружностями вершин зубьев и впадин. Обычно высоту зуба у конических колес с модулем т > 2,5 мм при черновом нарезании зубьев выполняют на 0,1-0,2 мм больше расчетной величины, чтобы предотвратить касание вершин чистовых резцов дна впадины зуба. Высота зуба складывается из высоты головки зуба и высоты ножки зуба hf. Различают внешнюю h, среднюю /г, внутреннюю hj и другие hx высоты зуба. Внешняя высота зуба измеряется по образующей дополнительного конуса.

Рабочая (граничная) высота зуба hi (см. рис. 42) - это высота зацепления двух зубчатых колес, равная сумме их головок.

Боковой зазор / (рис. 42) между зубьями в нормальном сечении задают в зависимости от модуля, условий работы передачи и выбирается по табл. 7. В результате погрешностей, возникающих при изготовлении, сборке и термической обработке, табличную величину бокового зазора обычно приходится увеличивать путем уменьшения толщины зуба, чтобы получить требуемый зазор при сборке. Как правило, колесо нарезают на теоретических установках двусторонней головкой, а боковой зазор увеличивают за счет уменьшения толщины зубьев шестерни.

Базовое расстояние А (см. рис. 42) - это расстояние от вершины делительного конуса до базовой плоскости, которая используется при сборке, контроле и в большинстве случаев при обработке зубчатого колеса. В - расстояние от вершины делительного конуса до плоскости внешней окружности вершин зубьев. Размеры А и В теоретические неизмеряемые; они точно учитываются при проектировании контрольной оснастки, наладке станков и т. д., С - расстояние от базовой плоскости до плоскости внешней окружности вершин зубьев. Этот размер оказывает неиосред-ственное влияние на форму заготовки, в чертеже он оговаривается допуском. Неточность размера С вызывает увеличение или уменьшение высоты зуба.

Корригирование конических зубчатых передач

Конические передачи, так же как цилиндрические корригируются. Практически некорригированных конических передач

Завстрент

Рис. 51. Параметры для корригирования:

в - оптимального профиля зуба; б - высоты зуба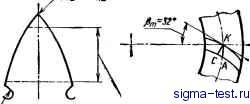

\ОптимальныО /Участок подрезания щрофит зуба

С прямыми и круговыми зубьями не изготовляют. Основная цель корригирования конических и цилиндрических передач состоит в том, чтобы подобрать такие коэффициенты пропорции зубьев, которые обеспечили бы оптимальный профиль зуба без участка подрезания в основании зуба и заострения вершины (рис. 51. а), а также достаточную прочность зуба на изгиб.

Высотная коррекция. Применяется при расчете геометрических параметров конических передач общего машиностроения. При высотной коррекции профиль зубьев шестерни получает положительный сдвиг, при котором высота головки зуба увеличивается на величину xm-fg, а высота ножки зуба на эту же величину уменьшается. Высота головки зуба колеса соответственно уменьшается и увеличивается высота ножки зуба:

Кг = !Ще + хгщ,; fi,i = /I - hi,

где f - коэффициент высоты головки зуба исходного контура; X - коэффициент смещения исходного контура.

Значения коэффициентов высоты головки зуба и смещения исходного контура для конических зубчатых колес определяют по графикам и таблицам, разработанным ЭНИМСом.

Если в цилиндрических передачах коэффициент смещения исходного контура х выбирают независимо от передаточного числа, то в конических передачах величина этого коэффициента для каждого передаточного числа различна. Каждому передаточному числу соответствует свой постоянный коэффициент смещения. При одинаковом числе зубьев шестерни и колеса коэффициент смещения исходного контура л: = 0.

При высотной коррекции с увеличением передаточного числа высота головки зуба шестерни постепенно увеличивается, а высота головки зуба колеса на ту же величину уменьшается. Сумма головок зуба колеса и шестерни при любом передаточном числз сохраняется постоянной, равной рабочей (граничной) высоте зуба

hi Ki + Ki-

3 Калашников С. Н.