сопряженного элемента. Направление линии зуба не влияет на плавность и эффективность работы передачи.

При работе конической и гипоидной передач передаваемая нагрузка раскладывается на две части: одна - вдоль оси - вызывает осевое давление на подшипники, другая - перпендикулярно оси - создает радиальную нагрузку на подшипники. Величина и направление осевых и радиальных нагрузок зависит от передаточного числа, угла зацепления, угла наклона зуба, направления линии зуба, направления вращения, а также от того, является ли шестерня ведущим или ведомым элементом.

Ведущая шестерня с левым наклоном зуба (рис. 46, а) при вращении в направлении по часовой стрелке I (если смотреть с заднего опорного торца) имеет тенденцию перемещаться по оси в сторону 2 от вершины делительного конуса, что способствует увеличению бокового зазора между зубьями. При вращении по часовой стрелке 3 шестерня перемещается в направлении 4 к вершине конуса, боковой зазор уменьшается, вызывая заклинивание, повышенный износ, а в отдельных случаях и поломку зубьев. Осевое перемещение 5 (рис. 46, б) шестерни с правым наклоном линии зуба будет направлено от вершины делительного конуса при вращении ее против часовой стрелки 6. Если направление вращения шестерни по часовой стрелке 7, то ее осевое перемещение 8 будет направлено к вершине делительного конуса.

Следовательно, направление линии зуба ведущей шестерни нужно выбирать такое, при котором осевая нагрузка на рабочем ходу способствует выходу шестерни из зацепления и увеличению бокового зазора. Надежность такой конструкции определяется упорными подшипниками, которые должны хорошо противостоять осевому смещению шестерни при передаче нагрузки.

Коэффициент перекрытия оказывает существенное влияние на плавную работу передачи и прочность зубьев. В конических и гипоидных передачах рассматривают три основных коэффициента перекрытия: торцовый, осевой и суммарный.

Коэффициент торцового перекрытия е - отношение длины линии зацепления к шагу на развертке дополнительного конуса. Для прямозубых конических передач общего машиностроения коэффициент торцового перекрытия всегда должен быть е > 1

Напрабиение перемещения

Рис. 46. Осевое перемещение шестерни в зависимости от направления ее вращения:

а - шестерня с левым и колесо с правым наклоном зубьев; б - шестерня с правым и колесо с левым наклоном зубьев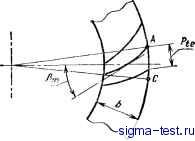

Рис. 47. Определение коэффициент! осевого перекрытия

а конических передач диффо ренциала 8 1,1. Ответстред ные прямозубые конический передачи изготовляют с коэффициентом профильного перекрытия 8 = 1,5 и более. Повышение этого коэффициента осуществляется путем увеличения высоты зуба и уменьшения угла зацепления.

Коэффициент осевого перекрытия Ер конических и гипоидных колес с круговыми зубьями равен отношению длины дуги АС (рис. 47) к внешнему окружному шагу зубьев. Минимальный коэффициент осевого перекрытия находится в пределах ер = = 1,5 -ь1,8, наилучшим коэффициентом с точки зрения эксплуатации является ер = 2 и более. Если, например, коэффициент осевого перекрытия ер = 2,3, то это означает, что в зацеплении одновременно находятся два-три зуба. Причем два из них полностью участвуют в работе, а третий зуб только на 30 %. Если коэффициент осевого перекрытия ер < 2, то в определенные моменты времени нагрузка в передаче передается только одним зубом.

Увеличения коэффициента осевого перекрытия можно достигнуть увеличением угла наклона зуба и ширины зубчатого венца, в также уменьшением модуля при соответствующем увеличении числа зубьев.

Суммарный коэффициент перекрытия характеризует суммарный коэффициент перекрытия под полной нагрузкой не на всей поверхности зуба, а на части, ограниченной поверхностью пятна контакта в форме эллипса. Этот коэффициент позволяет определить число зубьев, находящихся в постоянном контакте:

Максимальная плавность и бесшумность конических и гипоидных передач достигается при суммарном коэффициенте перекрытия е., = 2 и более.

Конусность зуба является важнейшим параметром, которая позволяет за счет ее рационального изменения выбрать более производительный метод нарезания зубьев, повысить период стойкости режущего инструмента и увеличить прочность зубьев. Большинство конических и гипоидных передач имеют конические зубья, высота которых от внешнего торца зуба к внутреннему уменьшается. Форма конусности зуба может быть различной, рассмотрим основные из них.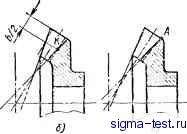

Рис. 48. Фор.мы конусности зуба:

с - стандартная; б - двойная; в - с поворотом линии конуса впаднн вокруг точки А;

г - равновысокий зуб

Стандартная конусность зуба (осевая форма зуба I, рис, 48,с) характеризуется тем, что образующие делительного конуса и конуса впадин пересекаются в одной точке. Высота и толщина зуба пропорционально уменьшаются по мере приближения к вершине конуса. Образующая конуса вершин не совпадает с вершиной делительного конуса и конуса впадин, а расположена параллельно образующей конуса впадин сопряженного колеса, благодаря этому радиальный зазор остается постоянным по всей длине зуба. В старых системах расчета образующие конусов вершин, делительного и впадин совпадали в одной точке, радиальный зазор уменьшался от внешнего к внутреннему торцу, соответственно уменьшался и радиус закругления в основании зубьев. Наличие постоянного радиального зазора позволяет увеличить радиус закругления в основании зуба, а следовательно, и прочность зубьев.

Конические и гипоидные передачи с постоянным радиальным зазором широко применяют в машиностроении. Зубья колеса нарезают двусторонними головками, обе стороны зуба обрабатывают одновременно, дно впадины имеет постоянную ширину. У сопряженной шестерни каждая сторона зуба нарезается отдельно односторонней резцовой головкой, ширина впадины зуба переменная.

Двойная конусность зуба (осевая форма зуба И) характеризуется тем, что образующие конуса впадин и делительного конуса не сходятся в одной точке. Разница между зубьями со стандартной и двойной конусностью показана на рис. 48, б. Сплошными линиями показано сечение зуба с двойной конусностью, штриховыми линиями - сечение стандартного зуба. Двойную конусность зуба можно получить путем поворота образующей конуса впадин вокруг любой точки вдоль длины зуба. Практически поворот образующей конуса впадин принято производить относительно двух точек: точки К (рис. 48, б), лежащей в середине ширины зубчатого венца, и точки А (рис. 48, в), расположенной на внешнем торце.